TD-Messungen am System Cu/Re(0001) von Ronald Wagner 

In dieser Arbeit werden Ergebnisse präsentiert, die aus der Untersuchung des Systems Cu/Re(0001) mittels Thermodesorptionsspektroskopie /TDS) gewonnen wurden. Dabei werden die Spektren einer genauen Kurvenformanalyse unterzogen. Als ein sehr gutes Werkzeug zur Untersuchung der dabei auftretenden Phänomene und Zusammenhänge hat sich die dreidimensionale Darstellung der Desorptionsrate in Abhängigkeit von Temperatur und Bedeckungsgrad erwiesen. Als Projektionen dieser Desorptionspfade in die Zustandebene (Q; T) sowie in die TD-Ebenen (T; R), (Q; R) ergeben sich die integrierten und die herkömmlichen TD-Spektren sowie die Layerplots. Die TD-Fläche wird aus den Isothermen und Isosteren, die aus den TD-Pfaden errechnet werden können und logarithmiert als Order- bzw. Arrheniusplots bekannt sind, gebildet. Die Desorptionsenergie wird nach den gängigen Methoden ermittelt und trägt zur Erklärung derEigenschaften des Systems bei.

Inhalt

1. Einleitung

2. Experimenteller Teil

3. Aufnahme der Meßwerte

4. Interpretation der Daten

4.1 TD-Formanalyse

4.1.1 Desorptionspfade

4.1.2 Desorptionsisothermen /-isosteren

4.2 Desorptionsenergieauswertung

4.2.1 Verwendete Auswertungsmethoden

4.2.2 Beurteilung der Ergebnisse

5. Diskussion der Ergebnisse

6. Literaturverzeichnis

1. Einleitung

Seit die ersten TD-Spektren von Apker im Jahre 1948 durchgeführt worden sind, hat sich in bezug auf die Meßpraktik aber auch auf die Auswertungsmethodik viel geändert. Der Einsatz der Computertechnik hat dazu einen großen Beitrag geleistet.

TD-Messungen stellen ein gutes Werkzeug dar, um energetische und kinetische Prozesse auf Oberflächen zu untersuchen. So ist es möglich, Aussagen über Wachstumsmoden adsorbierter Spezies zu tätigen, die Bindungsenergie von Adteilchen auf der Oberläche zu untersuchen und Informationen über die Wechselwirkungen der Adteilchen untereinander zu erhalten.

Gerade auf dem Gebiet der energetischen Auswertung von TD-Spektren haben sich zahlreiche Autoren verdient gemacht, wie z.B. Redhaed [RED62], King [K75/1], Bauer [B75/1], Habenschaden und Küppers [HAB83]. Aber auch die Form der Spektren wurden zu Aufklärung von Wechselwirkungen und Morphologien herangezogen [K95/2]. Zahlreiche Modelle wurden zur Beschreibung von TD-meßbaren Oberflächenphänomenen entwickelt, und oftmals wurden TD-Spektren simuliert.

Die Wahl der Substratoberfläche Re(0001) hatte folgende Gründe. Rhenium ist das Metall mit dem zweithöchstem Schmelzpunkt (3453K). Diese Eigenschaft ist bei TD-Versuchen natürlich sehr von Vorteil. Die (0001)-Oberfläche des hcp-Gitters des Rheniums weist eine sehr kleine atomare Korrugation entlang der dicht gepackten Reihen von etwa 0,1Å [PAR96] auf. Eine solche Fläche zu nutzen ist insbesondere dann günstig, wenn Approximationen eine glatte Oberfläche vorraussetzen. Mit einem Atomradius von 13.8nm ergibt sich eine Oberflächenatomdichte von r_2D=1,52x10¹⁵cm^-2.

Kupfer als Adsorbat bietet sich zum einen wegen seines relativ niedrigen Schmelzpunktes von 1358K an. Zum anderen sollten die Wechselwirkungen zwischen Kupfer und Rhenium ziemlich gering sein. Kupfer bildet ein fcc-Gitter aus. Der Misfit zwischen der (0001)-hcp-Fläche des Rheniums und der (111)-fcc-Fläche des Kupfers beträgt nur 7.6% zugunsten des Rheniums. Ausgeprägte Mischphasen aus Kupfer und Rhenium existieren nicht [HOL54]. Die maximale Löslichkeit von Rhenium in Kupfer ist 1 bis 2ppm [HEN69].

Auch die elektronischen Wechselwirkungen von Kupfer mit Rhenium sollten gering sein. Dies läßt sich durch einige allgemeine Betrachtungen grob abschätzen. Kupferatome besitzen ein halb besetztes 4s-Orbital. Im Rheniumkristall ist das 5d-Valenzband ebenfalls halb gefüllt. Beide Elemente sind also relativ elektronenarm, und es ergeben sich nur kleine elektronische Wechselwirkungen. Ein Elektronenfluß zur Angleichung der Fermi-Niveaus (Charge-Transfer) sollte klein sein. Die Elektronegativitäten nach Pauling unterscheiden sich ebenfalls kaum (Re 1,9; Cu 1,95). Goodman et al [G90/1, G91/2] fand in XPS-Untersuchungen fast gleiche Bindungsenergien der 2p_3/2-Elektronen des Kupfers auf der Re-Oberfläche und auf der Oberfläche von reinem Kupfer.

Im Kohlenmonoxid-Thermodesorptionsspektrum (CO-TDS) findet sich eine Verschiebung des Desorptionsmaximums zwischen reinem Kupfer und Cu/Re von nur +25K. Diese Ergebnisse deuten ebenfalls auf ähnliche Elektronendichten hin.

Untersuchungen ähnlicher Systeme sind in der Lieratur gut bekannt. Beispielsweise liegen Arbeiten von Günther et al [GÜN93] und Pötschke et al [PÖT91] zum Cu/Ru(0001) sowie von Bauer et al zum Cu/W(110) [B74/1, B86/2], Cu/Mo(110) [B87/1] vor. Weiterhin kann auf Erfahrungen mit der Re(0001)-Oberfläche von Rodriguez (Cu) [G90/1] und Schlatterbeck (Ag, Co) [S98/1, S98/2] zurückgegriffen werden.

2. Experimenteller Teil

Im Einzelnen soll hier nicht auf den experimentellen Aufbau eingegangen werden. Wir verweisen in diesem Zusammenhang auf frühere Publikationen [S98/1]. Die experimentellen Unterschiede zu [S98/1] sollen jedoch dargelegt werden.

Das Adsorbatmetall Kupfer wurde aus UHV-Dichtungen (Elektrolysekupfer mit einem Reinheitsgrad von 99,99%) der Firma VTS gewonnen. Es wurde bei einer Verdampfungstemperatur von 1030°C gearbeitet. Der Kupferdampfdruck betrug p=1,3x10^-4mbar. Die Zellentemperatur wurde elektronisch konstant (±1K) gehalten. Durch geringe Änderung der Temperaturvorgabe konnte die Aufdampfrate variiert werden. Typische Aufdampfraten lagen bei 1 bis 2ML/min. Meistens wurde bei einer Probentemperatur von 390°C gearbeitet, bei Temperversuchen bei bis zu 690°C.

Weiterhin soll im Folgenden speziell auf die Aufnahme der TD-Spektren eingegangen werden. Diese verlief voll rechnergestützt. Die linearen Heizrampen (2 bis 30 K/s) wurden vom Computer gesteuert und über einen Hertzregler an die Mittelspannungsversorgung der Elektronenstoßheizung übertragen. Die am meisten verwendete Heizrate war 7,7K/s, ein Wert, der ein Optimum in bezug auf die Auflösung und Intensität (bzw. Intensität-Rausch-Verhältnis) darstellt. Gleichzeitig wurde simultan zum Massenspektrometersignal die Thermospannung eingelesen. Je nach Meßmodus ist aus 20 bis 60 Meßwerten ein Mittelwert gebildet worden, so daß ein resultierendes Spektrum aus rund eintausend Meßpunkten bestand. Die Aufdampftemperatur des Substrates betrug 390°C.

3. Aufnahme der Meßwerte

Pro Serie wurden 20 bis 60 Spektren aufgenommen. Diejenigen Spektren, die sich wegen zufälliger Störeinflüsse nicht in die Serie einfügten, sind vernachlässigt worden. Die eingelesenen Werte der Thermospannung sind durch Extrapolation auf eine Wertetabelle (Thermospannung/Temperatur , Schrittweite 0.1mV/10K) erhalten worden. Von allen Rohspektren wurde zunächst der Untergrund subtrahiert. (Das geschah pauschal, indem die Werte der Grundlinie vor und nach der Desorption jeweils gemittelt wurden. Die Verbindungslinie dieser beiden Mittelwerte wurde als Grundlinie (Offset) vom Rohspektrum subtrahiert.) Geglättet wurden allgemein alle Endergebnisse, soweit dies nötig war; alle Zwischen-ergebnisse wurden jedoch ungeglättet weiterverwendet, damit keine Information verloren gehen konnte.Da das Signal des Massenspektrometers (TD-Spektrum) kein Absolutwert für die Bedeckungsgradänderung bzw. Desorptionsrate ist, sondern nur ein Relativwert, mußten alle Spektren auf den Wert Q=1 geeicht werden.Dies geschah folgendermaßen. Für jede Spektrenserie wurde die Desorptionsrate über dem relativen Bedeckungsgrad aufgetragen, der durch Integration der Thermodesorptionsspektren errechnet worden war. Der Eichquotient ist dabei genau der größte Schnittpunkt eines Spektrums mit der Bedeckungsgradachse, das noch allein dem ersten Zustand zuzuordnen ist.

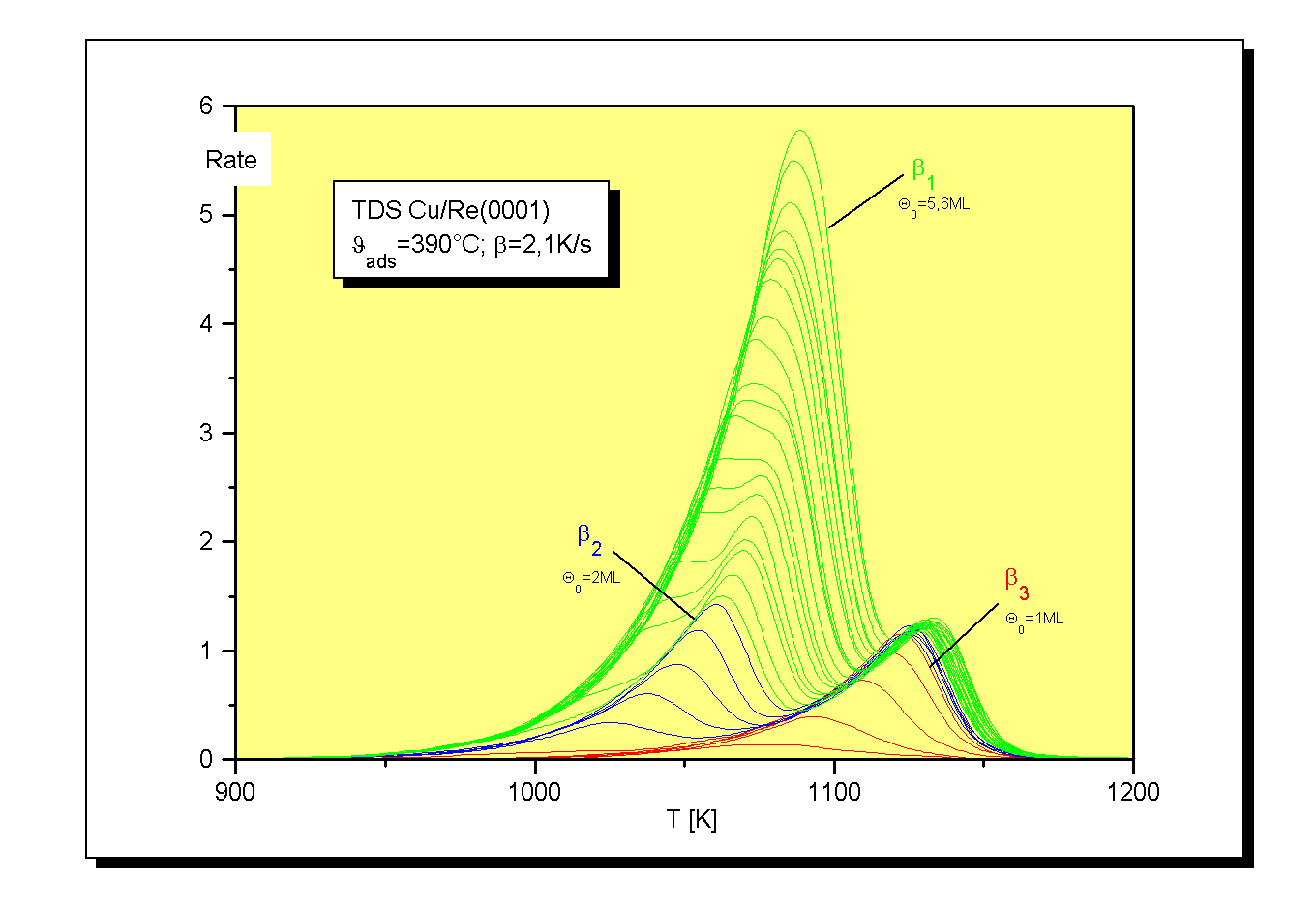
Abb.1 zeigt die Thermodesorptionsspektren bis zu einem Anfangsbedeckungsgrad Q₀ von 6ML.

Abbildung 1

Es sind deutlich drei Desorptionszustände zu erkennen, b₁, b₂ und b₃. Der b₃-Zustand bildet sich (bei der gewählten Heizrate von 7,7K/s) ab T=1020K aus und hat sein Maximum (Q₀=1ML) bei T=1120K. Der b₂-Zustand entwickelt sich bei T=950K und hat ein Maximum (Q₀=2ML) bei T=1055K. Der dritte Zustand, b₁, beginnt bei T=940K und hat ein Maximum (Q₀=3ML) bei T=1035K. Dieser Zustand gewinnt mit zunehmender Anfangsbedeckung sehr stark an Größe, so daß er, bei einer Anfangsbedeckung von etwa Q₀=6ML den b₂-Zustand überdeckt. Wie weitere Untersuchungen zeigten, wird, bei etwa Q₀=20ML, auch der b₃-Zustand überdeckt. Der b₁-Zustand und der b₂-Zustand liegen etwa im gleichen Temperaturbereich der Niedertemperaturseite des Spektrums, jedoch in größerer Entfernung zum b₃-Zustand. Das weist bereits darauf hin, daß der b₁-und der b₂-Zustand energetisch ähnlich sind. In den Arbeiten von He [G90/2] und Rodgriguez [G92/1] sind nur der b₁ und der b₃- Zustand zu erkennen, ein Umstand, der durch eine schlechtere Auflösung bei den Messungen zu erklären ist.

Durch eine Verkleinerung der Heizrate b verkleinern sich nicht nur die Maximumstemperaturen der Zustände, sondern auch die Intensitäten der Spektren bei gleichzeitiger Vergrößerung der Auflösung. Wird die Heizrate jedoch zu klein gewählt, verschwindet das Signal schließlich im Untergrund.Sowohl bei Messungen mit kleinerer Heizrate (b=2,1K/s), als auch bei Versuchen mit höherer Aufdampftemperatur (690K) ergab sich die gleiche Spektrenform.

Besonderes Augenmerk galt der Ausbildung eines eventuellen vierten Peaks beim Übergang zur vierten Monolage. Die Flanken der Spektren zeigen jedoch keine Schultern oder gar neue Maxima, was darauf schließen läßt, daß sich die Ausbildung einer weiteren Lage nicht als neuer Zustand in diesem Gebiet dokumentiert. In Untersuchungen des Systems Ag/Re(0001), die unter gleichen Bedingungen und an der gleichen Apparatur ausgeführt wurden, waren durchaus Unregelmäßigkeiten in der betrachteten Flanke zu erkennen [S98/1].

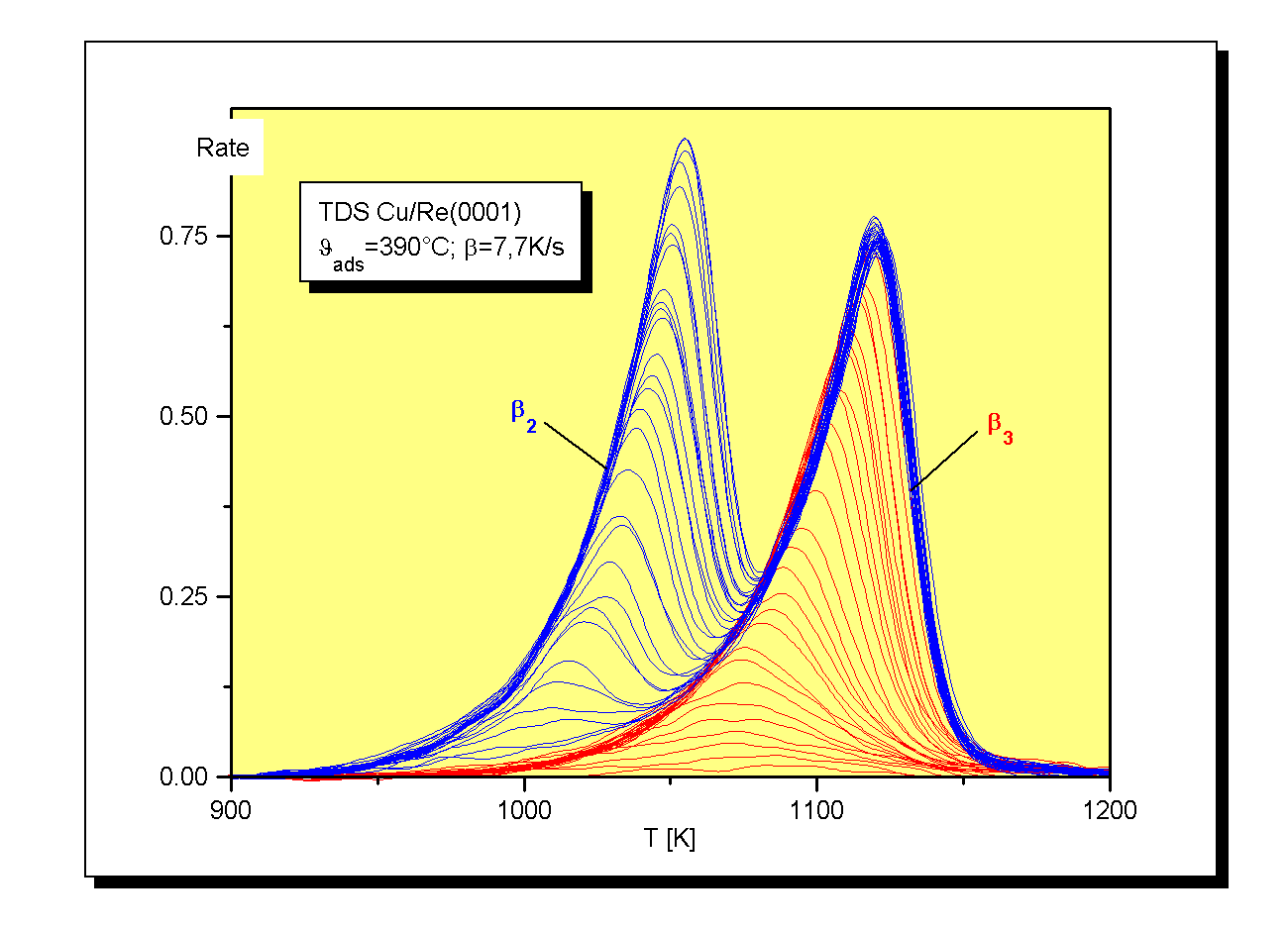Abbildung 2

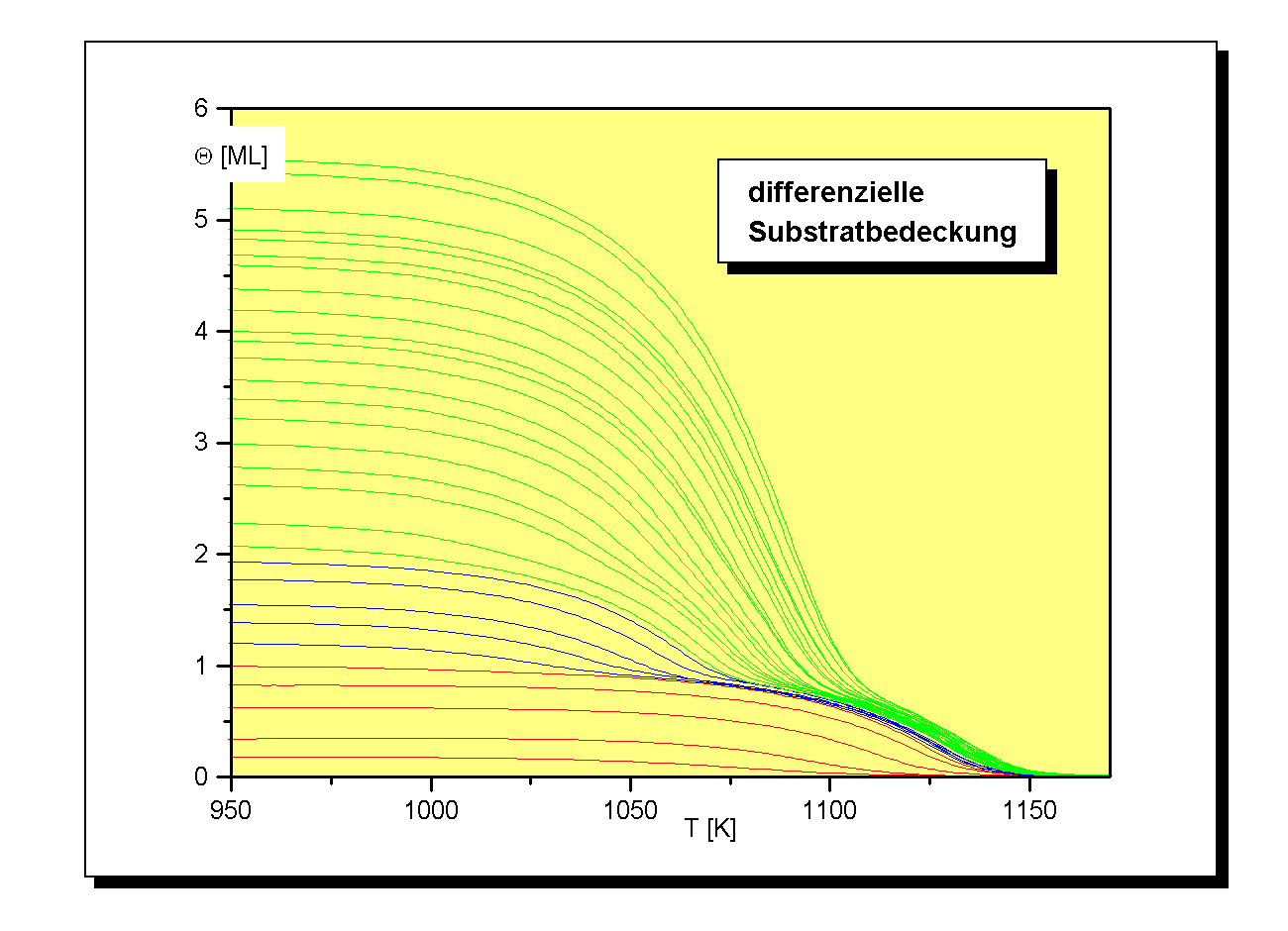
Zur genaueren Untersuchung der ersten beiden Lagen wurde eine weitere TD-Serie aufgenommen, s. Abb.2.

Wie aus Abb.1 und Abb.2 zu erkennen ist, fallen die Anstiegsflanken gleicher Zustände aller Spektren (zu unterschiedlichen Anfangsbedeckungen) zusammen. Dies ist besonders gut beim b₁-Zustand ersichtlich. Die Niedertemperaturflanken aller Spektren bilden bis zur Temperatur T_g eine gemeinsame Linie. Danach wird der Anstieg der individuellen Spektren kleiner, und sie verlassen die Flanke. Nach dem Passieren des Maximums bei T_max laufen sie gegen null.

Dieser Effekt der ‘gemeinsamen Anstiegsflanke’ ist kennzeichnend für eine Desorption nullter Ordnung [N86/1], [N91/1], [CHR91]. Kreuzer [K95/2] beschreibt allerdings auch weiter, daß durch Interschichtwechselwirkungen solche Effekte vorgetäuscht werden können. Nichtsdestoweniger ist die vorliegende Kurvenform ein deutliches Indiz für eine Desorption nullter Ordnung. Eine solche Desorptionsordnung kann Indiz für eine Desorption mit vorgelagertem Gleichgewicht sein. Dieses kann innerhalb von Lagen durch einen zweidimensionalen Phasenübergang errreicht werden [W98/2] oder durch die Desorption von dreidimensionalen Kristalliten. Im vorliegenden Fall gehen wir davon aus, daß sich zunächst zwei Lagen auf der Oberfläche ausbilden, auf der dann Kristallite aufwachsen. Dies würde einem Quasi-SK-Wachstum entsprechen [STR38]. Ein solches Verhalten wurde durch STM-Aufnahmen von Günther et al [GÜN93] für das System Cu/Ru(0001) gefunden.

Da der Verlauf der Spektren für sehr kleine Bedeckungen aus den Abb.1 und Abb.2 nicht genau zu erkennen ist, wurde eine weitere Spektrenserie (Abb.3) aufgenommen. Es ist hier eine relativ hohe Heizrate gewählt worden (b=21,7K/s), da im Bereich dieser kleinen Anfangsbedeckungen die Intensität der Zustände sehr gering ist.

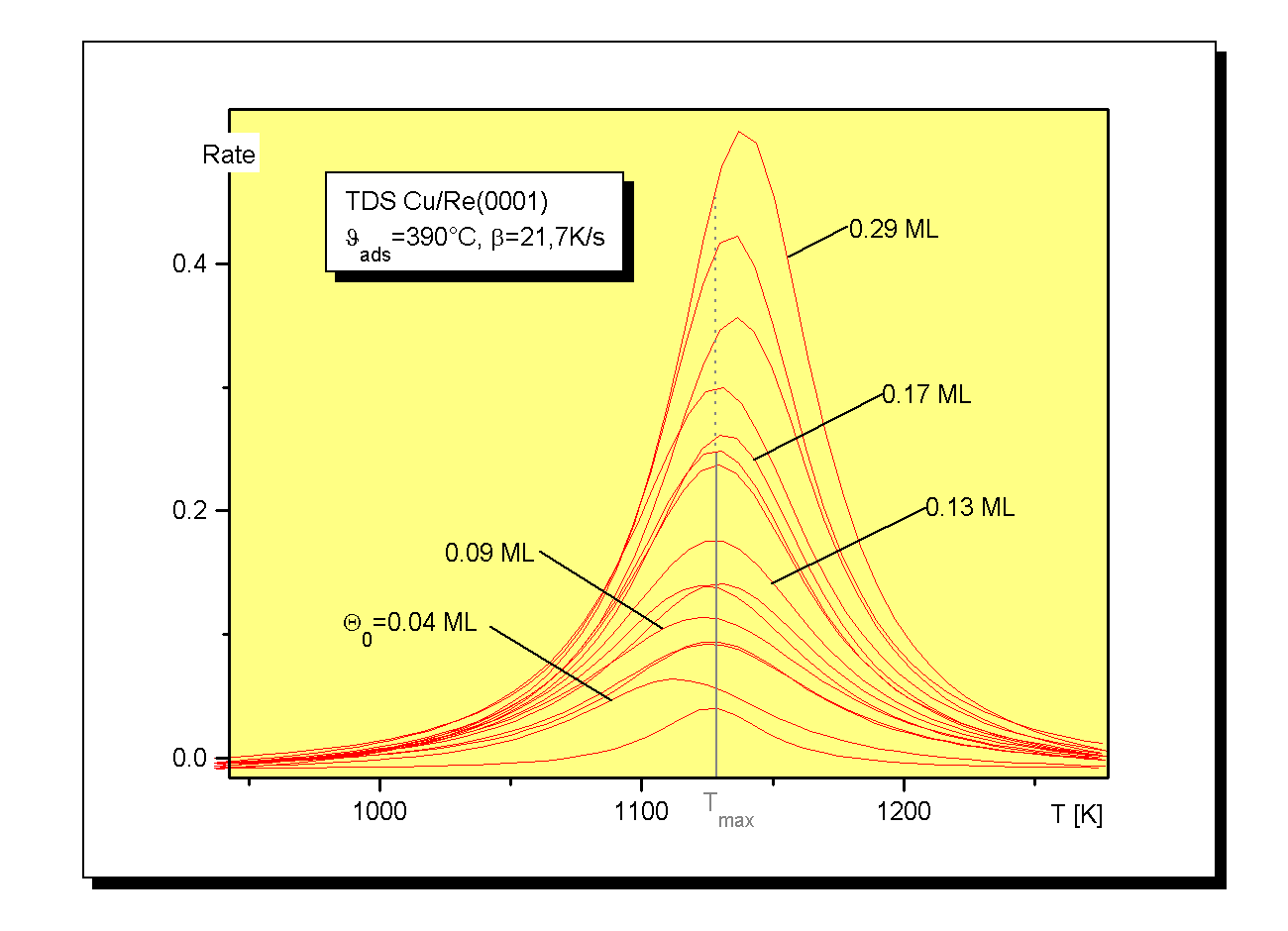Abbildung 3

Die Ausbildung eines weiteren Zustandes ist auch hier nicht zu erkennen. Ein anderer Fakt wird aber deutlich. Entgegen dem Verhalten der Desorptionsspektren zu höheren Anfangsbedeckungen verändert sich hier die Maximumstemperatur nicht. Für alle Spektren bis Q₀=0,15ML wird bei der gewählten Heizrate der Wert T_max=1127K erhalten. Hier ist also der Effekt der gemeinsamen Flankenbildung nicht erkennbar. Wie oben ausgeführt, liegen sogar die Desorptionsmaxima übereinander, was auf eine Desorptionsordnung von n=1 hinweist. (Diese Zuordnung geht bereits auf Redhaed [RED62] zurück. Er nutzte die konstante Maximumstemperatur sogar aus, um mit ihrer Hilfe die Desorptionsenergie abzuschätzen.) Im Bereich sehr kleiner Bedeckungen liegt also eine Desorption erster Ordnung vor. Dieser Befund ordnet sich sehr gut in die o.a. Aussagen ein, daß sich im Bereich der ersten Lage ein Zeidimensionales Phasengleichgewicht einstellt [W98/2].

4. Interpretation der Daten

4.1 TD-Formanalyse

Wie in Abschnitt 3 demonstriert, ist es möglich, aus einer genauen Analyse der TD-Kurvenformen ein Vielzahl von Aussagen zu erhalten. Durch die Untersuchung von TD-Serien wird diese noch potenziert. Eine weitere Erhöhung der Informationsfülle wird dadurch erreicht, daß man die Sichtweise auf die gemessenen Daten verändert und Zusammenhänge zwischen diesen Projektionen berücksichtigt. Das soll im Folgenden demonstriert werden.

4.1.1 Desorptionspfade

Durch die Integration der Werte der Desorptionsrate von der Hochtemperaturseite bis zur Temperatur T können Wertetripel () gewonnen werden. Man erhält so temperaturabhängige Bedeckungskurven.Einem jeden Ratenwert ist somit die momentane Substattemperatur und -bedeckung zugeordnet.

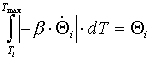(T) (1)

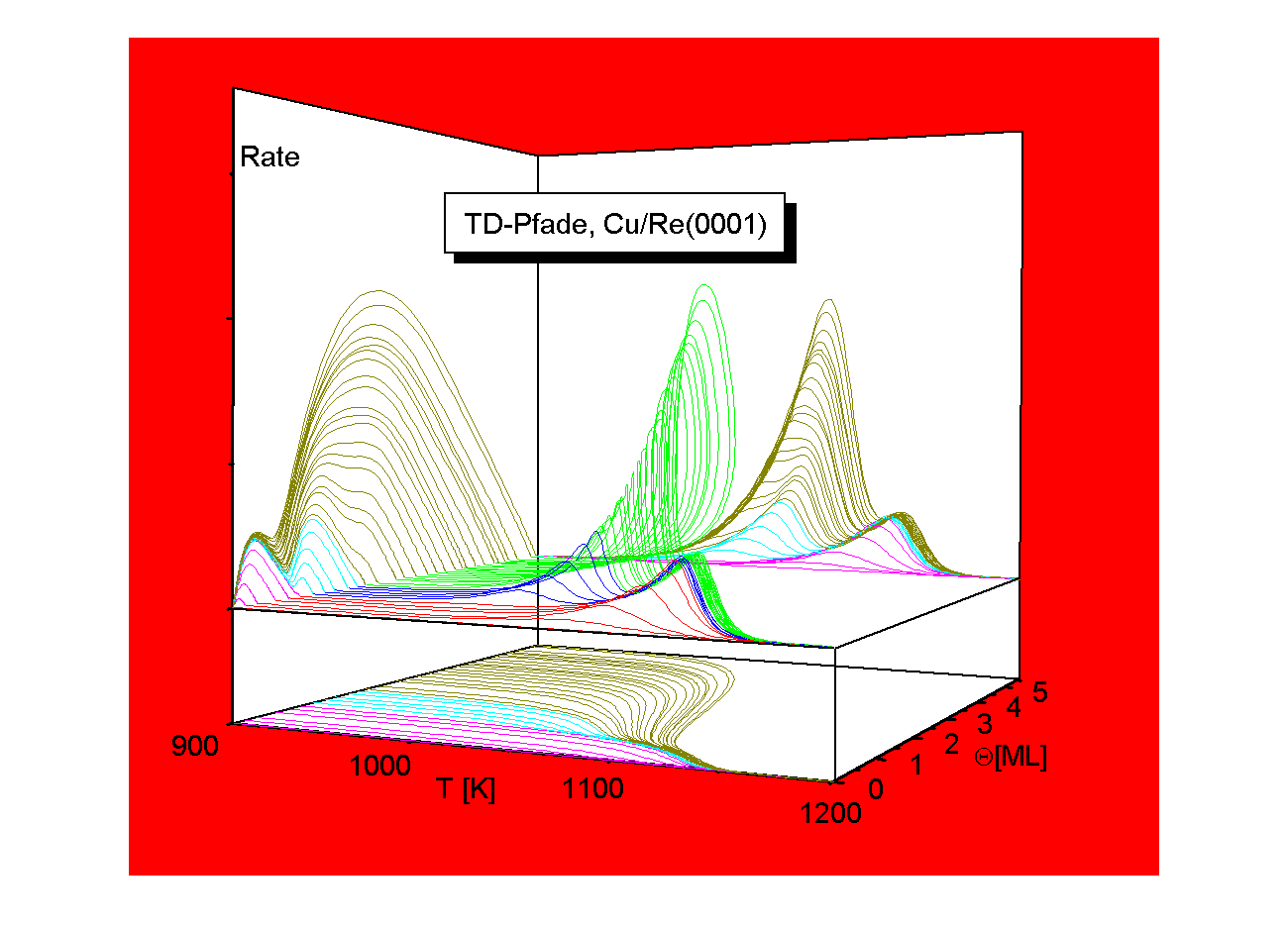Abbildung 4

Um die volle Aussagekraft der Wertetripel zu erhalten, ist es möglich und nötig, die daraus gebildete Desorptionsratenfunktion in Abhängigkeit der zwei Variablen Temperatur und Bedeckungsgrad R=-dQ/dT=f(T, Q) dreidimensional darzustellen. Dies ist in Abb.4 für die TD-Spektren aus Abb.1 dargestellt. Hier sind die TD-Spektren zu verschiedenen Anfangsbedeckungen zu ‘TD-Pfaden’ geworden, die den Weg der Thermodesorption über die ‘TD-Fläche’ beschreiben. Die einzelnen Zustände sind hier sehr schön separiert und können aus beliebig vielen verschiedenen Blickwinkeln betrachtet werden.

Abbildung 5

Die Projektionen der Pfade in die ‘Zustandsebene’ (Q, T) sowie in die ‘Desorptionsraten-ebenen’ (Q, R), (T, R) sind ebenfalls mit eingezeichnet. Die Zustandsebene verdeutlicht hierbei den thermodynamischen Aspekt des Systems, da es durch den Bedeckungsgrad und die Temperatur jederzeit vollständig beschrieben wird. Die Projektion in diese Ebene sind die integrierten TD-Spektren (Abb.5). Aus ihnen kann man nach Kreuzer [K95/2] insbesondere Ausssagen über die Wechselwirkungen unterschiedlicher Adsorbatschichten treffen. Außerdem lassen sich in dieser Ebene Phasengrenzen und Phasenübergänge darstellen [W98/2].

Abbildung 6

Als Projektrion in die Desorptionsratenebene (T, R) erhält man wieder die ursprünglichen, gemessenen TD-Spektren. Hieraus ist die Überlegenheit der dreidimensionalen Darstellung zu erkennen. Innerhalb der normalen TD-Spektren erhält man nur Aussagen über den Verlauf der Desorptionsrate mit der Temperatur, wobei man keinerlei Aussagen über den Bedeckungsgrad machen kann, außer daß er sich verringert.

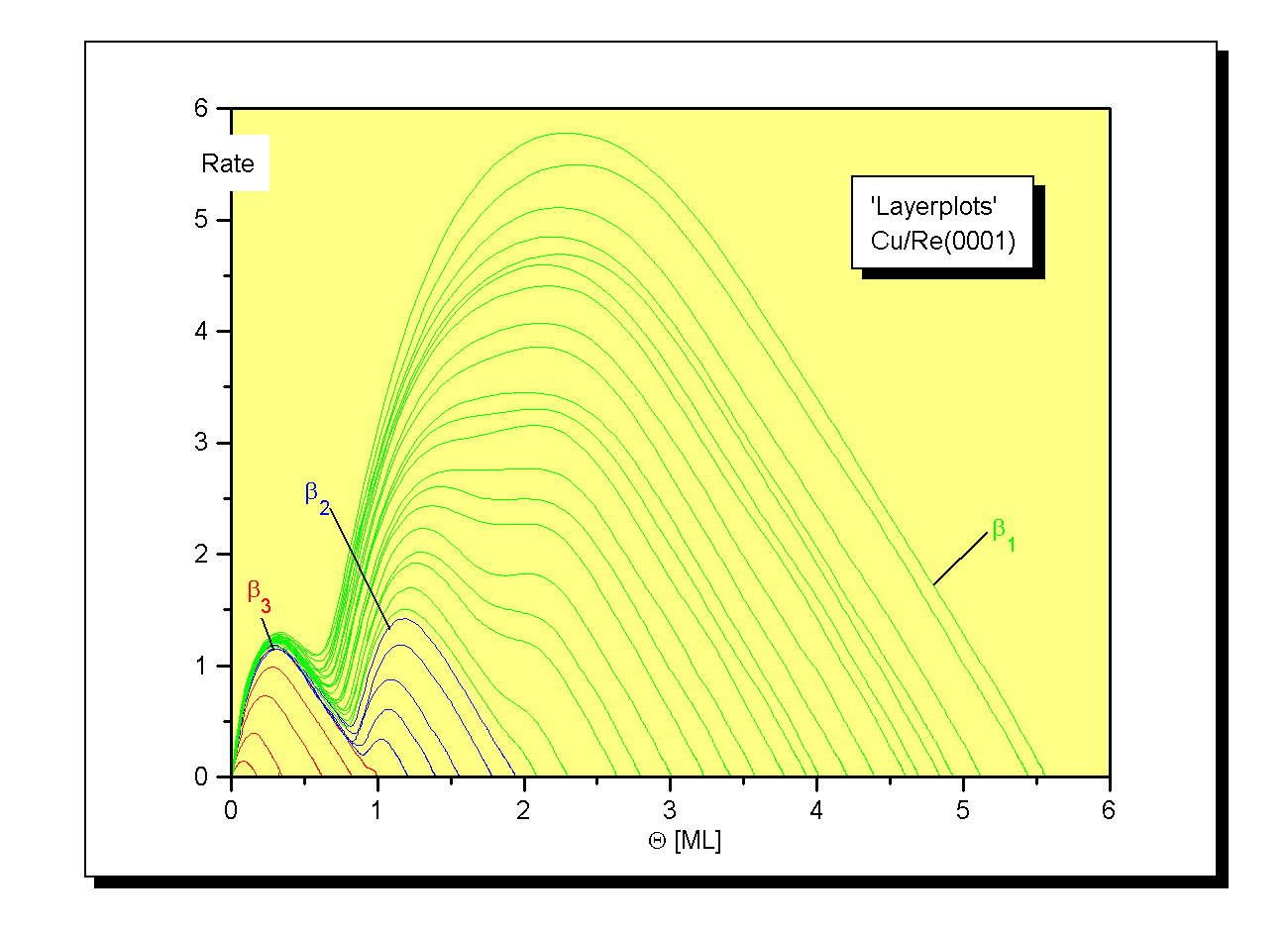
Äquivalent verhält es sich bei den ‘Layerplots’ [M92/1], die die Prtojektion in die die Desorptionsratenebene (Q, R) darstellen (Abb.6). Die Desorption vollzieht sich in dieser Darstellung von rechts nach links. In einem weiten anfänglichen Bereich zeigen fast alle Spektren (hauptsächlich die mit mittleren bis großen Lagenbedeckungen) einen konstanten Anstieg. Dies ist ein Zeichen für eine Desorption nach nullter Ordnung.

4.1.2 Desorptionsisothermen /-isosteren

Bis hier wurden die tatsächlichen TD-Pfade betrachtet, die in guter Näherung mit der Polanyi-Wigner-Gleichung beschrieben werden konnten.

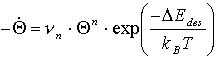(2)

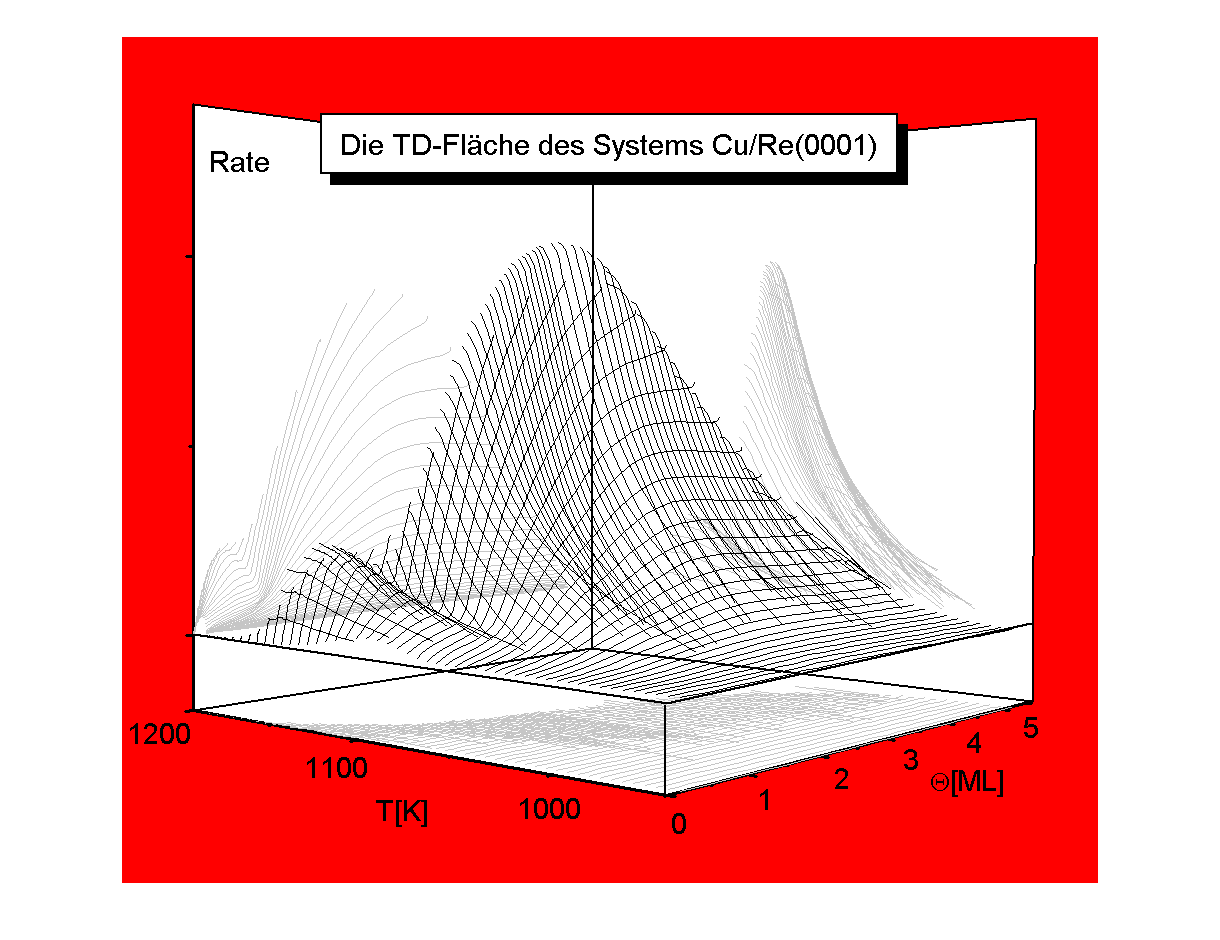Abbildung 7

Wie schon oben ausgeführt, hat man es hier mit einer Funktion zu tun, die von zwei Variablen abhängt, nämlich vom Bedeckungsgrad und von der Temperatur. Durch Parametrisierung jeweils einer der beiden Variablen gelangt man zwanglos zu Gleichungen für die isostere und die isotherme Desorption. Die TD-Pfade aus Abb.4 wurden einer solchen Umwandlung unterzogen. Praktisch geschah dies numerisch dadurch, daß alle Wertetripel nach dem Bedeckungsgrad bzw. nach der Temperatur geordnet wurden. Das Ergebnis ist die durch ein Gitternetz gegebene TD-Fläche, die in Abb.7 dargestellt ist. Innerhalb der insgesamt gekrümmten TD-Fläche sind Gebiete zu erkennen, die eine (in Q-Richtung exponentiell gekrümmte und) in T-Richtung gerade Fläche darstellen. Dies ist wiederum ein Indikator für eine Desorption 0. Ordnung in diesen Gebieten.

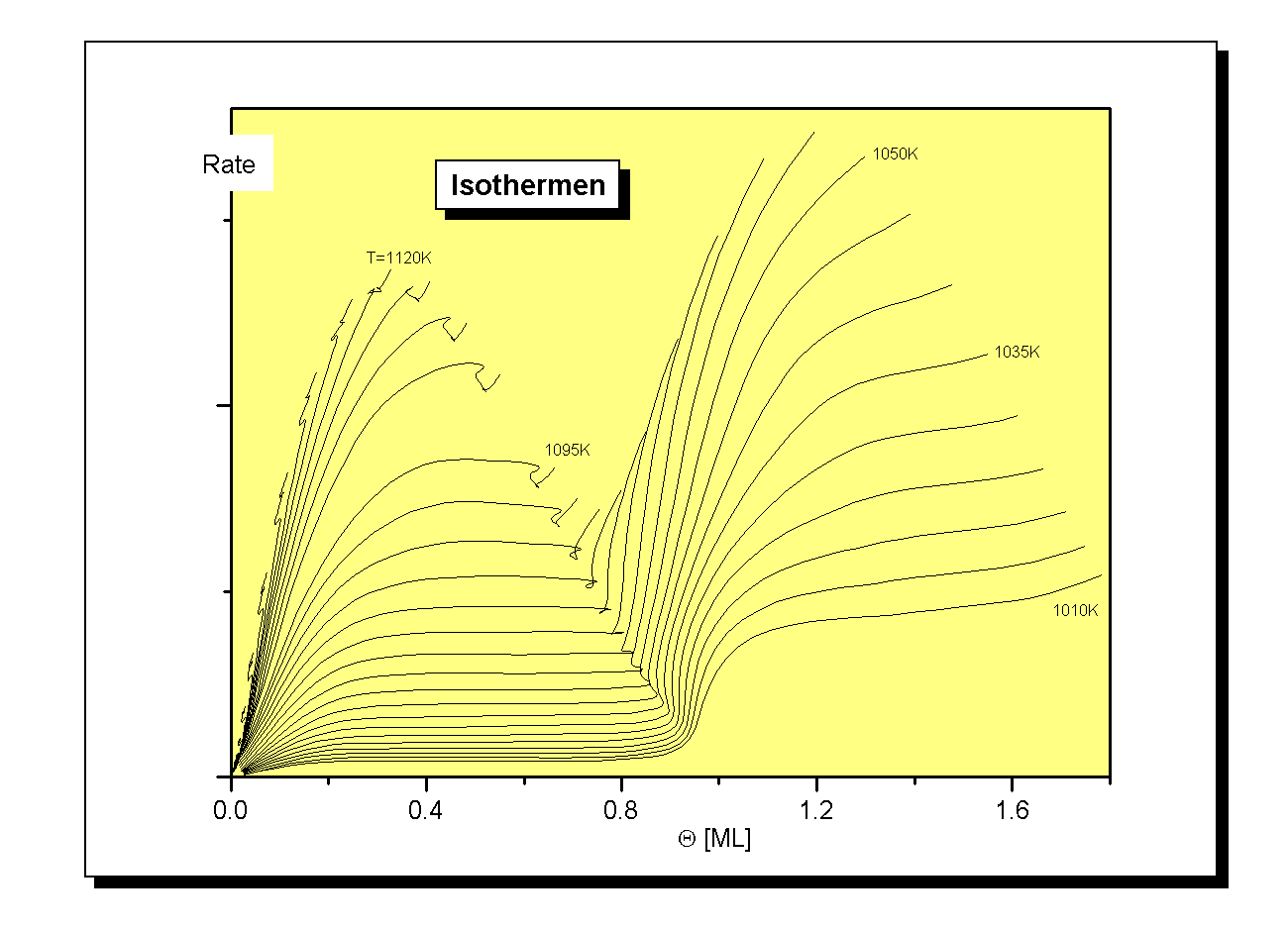Abbildung 8

Insbesondere dokumentiert sich diese Flächenform in der (Q; R)-Projektion, die die Darstellung der isothermen Desorption (T=param.) ist (Abb.8). Hier ist der gerade Flächenabschnitt durch einen konstanten Verlauf der Isothermen in diesem Bereich gekennzeichnet. Der Übersichtlichkeit halber sind in Abb.8 die Isothermen nur für die ersten beiden Lagen dargestellt.

Bei der Formulierung einer Isothermen Desorptionsrate (also einer Desorption bei konstanter Temperatur) drängt sich die Frage nach dem dazugehörigen Experiment auf. Tatsächlich werden solche Experimente durchgeführt. Bauer et al [B88/1] haben die direkt gemessenen Werte mit den aus TD-Spektren erhaltenen verglichen und eine gute Übereinstimmung festgestellt. Dabei wurde die Probe auf einer konstanten Temperatur im Intervall der Desorption gehalten und mit Adsorbatmaterial bedampft. Zum Zeitpunkt t=0 wurde der Teilchenstrom abgeschaltet und das resultierende Spektreum aufgezeichnet.Eine interessante Anwendung der Formulierung von Isothermen ist deren doppeltlogarhitmische Darstellung, die gemeinhin als ‘Orderplot’ bezeichnet wird (Abb.9).Aus der logarhytmierten Form der Polanyi-Wigner-Gleichung

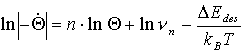(3)

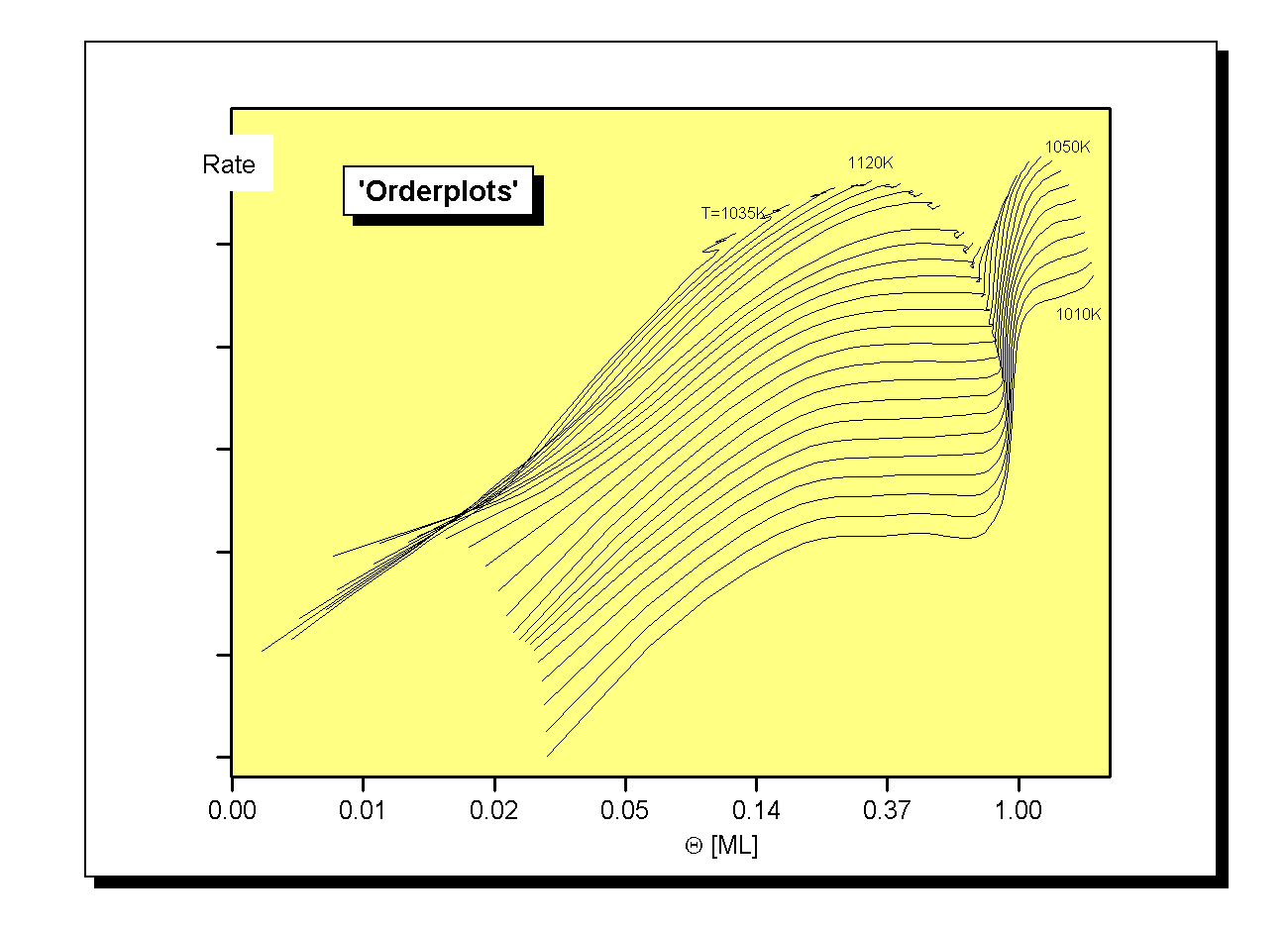
ist sofort erkennbar, daß aus dem Anstieg der dazu gehörigen Kurven direkt die Desorptionsordnung n zu entnehmen ist.

In Abb.9 sind hauptsächlich drei Abschnitte zu erkennen, die einer gemeinsamen Steigung zuzuordnen sind. Besonders klar sind die Verhältnisse bei der Isotherme zu T=1010K. Diese hat zwei Abschnitte, in denen der Anstieg null ist. Im letzten Teil (Q < 0,15ML) ist der Anstieg etwa eins.

Abbildung 9

Die anderen Isothermen zeigen das gleiche Verhalten, mit der Einschränkung, daß mit steigender Temperatur die Anzahl der Gebiete mit konstanter Steigung abnimmt. Dies ist verständlich, wenn man bedenkt, daß mit ansteigender Temperatur mehr und mehr Zustände desorbieren und zur Darstellung nicht mehr beitragen können.

Es ist also festzustellen, daß für den Bereich mit Q < 0,15ML eine Desorption erster Ordnung vorliegt. Ab Q=0,15ML wird die Desorptionsordnung null, bis eine Bedeckung von Q=1 erreicht ist. Diese Tatsache kann mit einem schon oben erwähnten zweidimensionalen Phasenübergang erklärt werden [W98/1]. Die gleiche Erklärung kann auf den konstanten Verlauf innerhalb der zweiten Lage angewendet werden. Einen gleichen Verlauf der ‘Orderplots’ erhält Nagai [N86/1] für den Übergang von n=1 zu n=0 simulierter Spektren.

Abbildung 10

Nicht eingezeichnet in Abb.9 ist der Verlauf für die dritte bis n-te Lage (Multilage). Dieser ist ebenfalls parallel zur Q-Achse. Vom horizontalen Teil der Kurve für die zweite Lage ist er durch einen Anstieg, äquivalent dem vom Übergang von der ersten zur zweiten Lage getrennt. Bei weiteren Übergängen (3/4, 4/5, usw.) treten allerdings keine weiteren Sprünge auf. Daraus kann gefolgert werden, daß hier ein Wachstumsmodus vorliegt, bei dem nicht zwischen einzelnen Zuständen (Lagen) differenziert wird. Dies wäre bei der Ausbildung von 3D-Kristalliten der Fall.

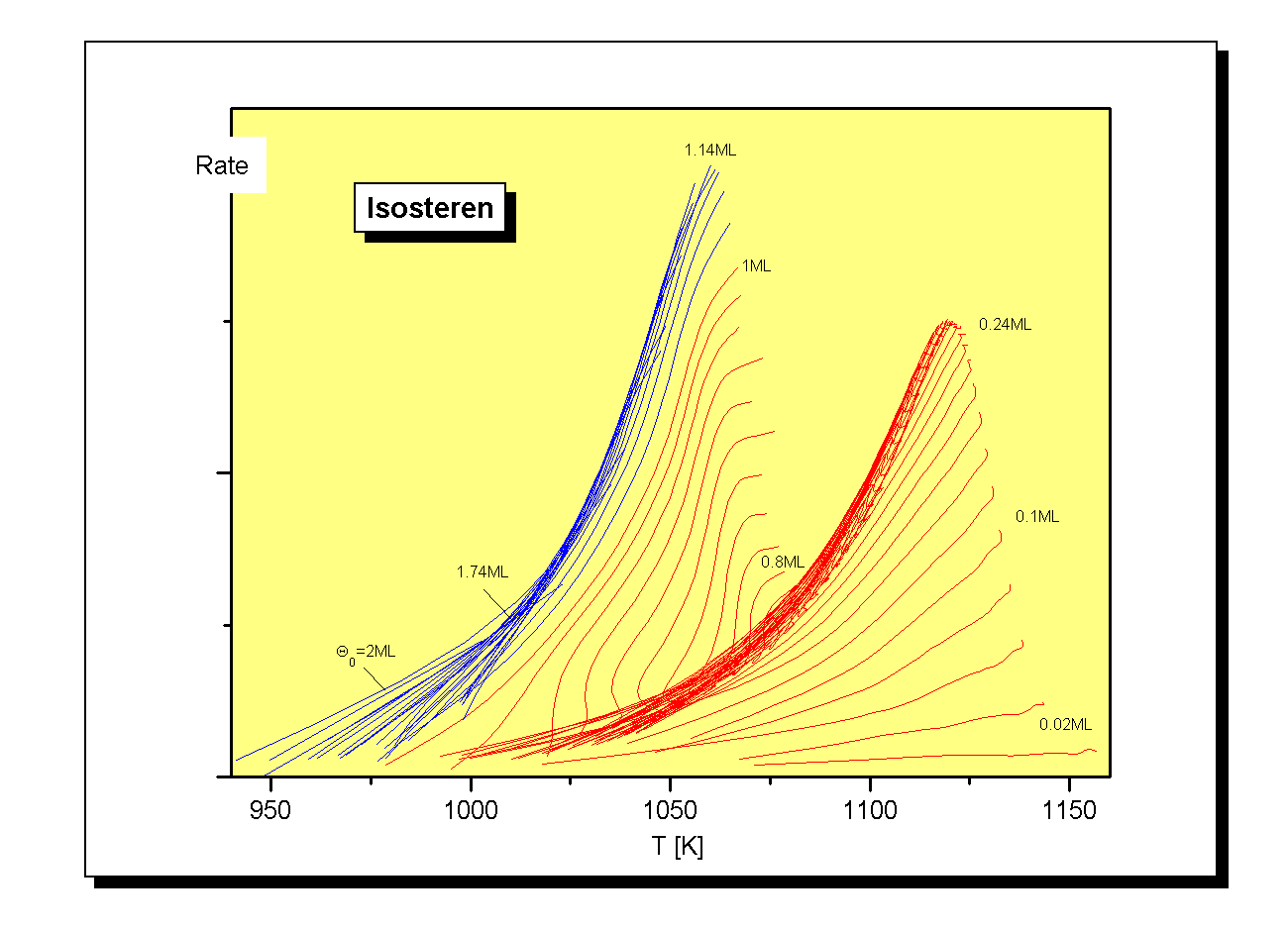
Die zweite Projektionsmöglichkeit der TD-Fläche ist die in die die Desorptionsratenebene (T, R). Dadurch erhält man die in Abb.7 mit eingezeichneten Desorptionsisosteren, die zur deutlicheren Veranschaulichung in Abb.10 direkt dargestellt sind. Auch bzw. gerade hier stellt sich die Frage nach dem experimentellen Pondon. Die Desorptionsrate ist ja gerade als Änderung des Bedeckungsgrades definiert. Diese Definition müßte man für eine experimentelle Durchführung insoweit umändert, als daß die Desorptionsrate jetzt mit dem sich von der Probe wegbewegendem Partikelstrom identifiziert wird. Praktisch müßte dieser Partikelstrom detektiert werden und gleichzeitig durch einen differenziell gleichen negativen Partikelstrom zum Konstanthalten des Bedeckungsgrades kompensiert werden. Dies könnte durch ein geregeltes Bedampfen geschehen. Dabei müßte, wie beim eigendlichen TD-Experiment die Temperatur linear erhöht werden.

Die in Abb.10 dargestellten Isosteren bis zu einem Bedeckungsgrad von 2ML können grob in vier Gruppen eingeteilt werden. Die erste Gruppe von 0 bis 0,25ML sowie die dritte Gruppe von 0,76ML bis 1ML füllt jeweils ein großes Gebiet der Desorptionsratenfläche, wobei es bei der dritten Gruppe zu starken Steigungswechseln kommt. Die beiden anderen Gruppen (0,26ML bis 0,72ML und 1.04ML bis 2ML) laufen jeweils in einer gemeinsamen Anstiegsflanke. Dieses Verhalten ist einer Desorption nullter Ordnung zuzuschreiben. Für die Gruppen eins und drei müssen besondere Effekte zum Tragen kommen.

Abbildung 11

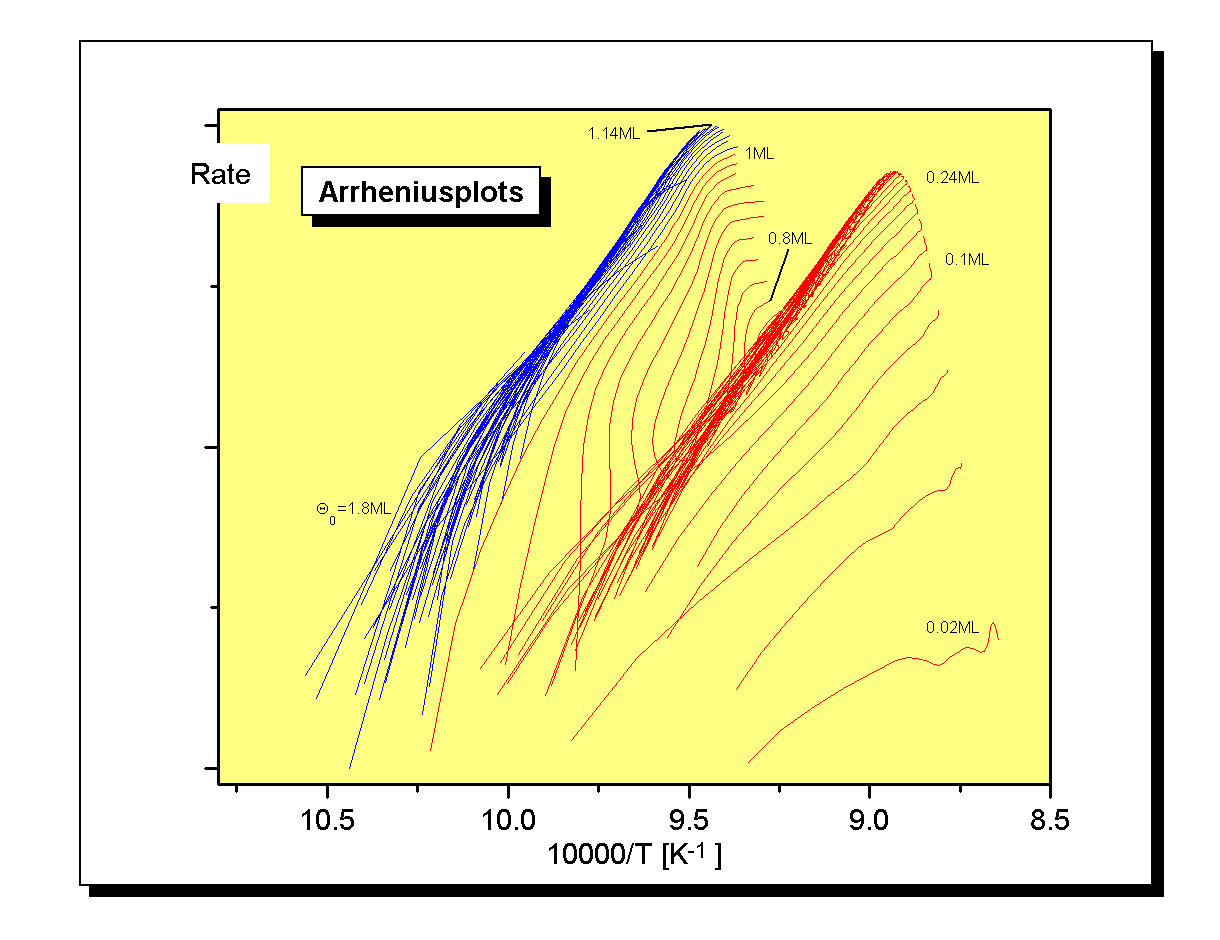
Auch die Darstellung der Isosteren hat eine weitere, oft benutzte Anwendung, deren Aussagekraft oft unterschätzt wird. Stellt man nämlich die Bedeckungsgradachse logarithmisch und die Temperaturachse reziprok dar, erhält man die ‘Arrheniusplots’, aus denen als ‘Geraden-parameter’ die Desorptionsenergie und der Frequenzfaktor für die Desorption entnommen werden kann [K75/1]. Die aus Abb.10 gewonnenen Arrheniusplots sind in Abb.11 dargestellt.

 Die Isosteren der Gruppe zwei und vier zeigen hier einen jeweils annähernd gleichen geraden Verlauf und sollten einen konstanten Verlauf der Desorptionsenergie in diesem Bedeckungsgradbereich verursachen. Die Isosteren der Gruppe eins sind auch annähernd linear, ihr Anstieg vergrößert sich jedoch. Die Folge davon sollte ein Anstieg der Desorptionsenergie sein. Die Isosteren der Gruppe drei zeigen kein einheitlich lineares Verhalten, ihr Verlauf kann aber in drei lineare Abschnitte eingeteilt werden. Zunächst besitzen sie einen sehr starken Anstieg, im mittleren und im letzten Bereich ist der Anstieg jeweils geringer. Die Isosteren der Gruppe 3 mit kleinen Bedeckungsgraden werden eher vom Bereich des kleinen Anstieges dominiert. Bei denen mit höheren Bedeckungsgraden überwiegt der Bereich des größeren Anstiegs. Als Folge dieser Nichtlinearität läßt sich der Verlauf der Desorptionsenergie in diesem Bedeckungsgradgebiet nur schlecht voraussagen. Er sollte durch starke Änderungen gekennzeichnet sein.

Wenn sich die Kurven, wie in Gruppe drei nicht durch einheitliche Geraden darstellen lassen, kann das mehrere Ursachen haben [W97/1]:

• das Vorhandensein von mehr als einem Adsorptionsplatz,
• das Auftreten von Quanteneffekten, die eine Temperaturabhängigkeit von n bedingen können (Physisorptionszustände),
• ein zweidimensionaler Phasenübergang [W98/2],
• Misfit-Gitteranpassungen.

4.2.1 Verwendete Auswertungsmethoden

Eine Möglichkeit, DE_des zu bestimmen, ist die Messung der heizratenabhängigen Lage des Peakmaximums (Heizratenvariation). Ausgehend von der Voraussetzung, daß es sich um eine Desorption nullter Ordnung handelt, erhält man die Polanyi-Wigner-Gleichung in der bedeckungsgradunabhängigen Form, die man, nach Einführung der Heizrate und unter Ausnutzung der Tatsache, daß die Desorptionsrate sich bei der Peakmaximumstemperatur T_max nicht ändert, in die folgende Gleichung umwandeln kann:

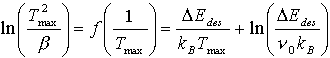(4)

Bei der graphischen Darstellung der Funktion erhält man eine Gerade, aus der die Arrheniusparameter gewonnen werden können. Da Christmann [CHR91] für die Heizratenvariation von Desorptionen erster Ordnung den selben Term angibt, ist diese Auswertemethode zur Auswertung von Metall-TD-Spektren prädestiniert. Bei der Heizratenvariation wird jeweils die Maximumstemperatur zur Rechnung benutzt. Andere Spektren können, allerdings nicht sehr stark wechselwirken. Auf Grund der hohen Signalintensität besitzt diese Methode ein besonders gutes Signal-zu-Rausch-Verhältnis. Ein numerisches Verfahren nach Schlatterbeck [S98/1], das auf dem Auswertungsverfahren nach Bauer [B75/1] basiert, stellt eine sehr genaue Untersuchungsmethode für die Bedeckungsgradabhängigkeit der Desorptionsenergie dar. Hierbei wird zunächst aus den Wertepaaren (Q; ) die Lebensdauer berechnet.

t(Q, T) (5)

Man erhält so neue Wertetripel (T; Q; t) und daraus, wie o.a. Isosteren, die als Arrheniusplots dargestellt werden können:

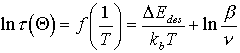(6)

(Zum Bereich bis Q=1ML wurden nur die TD-Spektren mit Q₀<1 berücksichtigt.)

Bei dieser Methode wird nicht nur der gesamte Spektrenbereich der Analyse unterzogen, sondern auch mehrere Spektren einer Serie. Daraus resultiert ein geringes Rauschen der Daten, aber Effekte z.B. beim Übergang zwischen zwei Lagen fallen besonders stark ins Gewicht. Die Ergebnisse dieses Verfahrens unterscheiden sich nicht von denen, die durch Nutzung der Desorptionsrate anstelle der Lebenszeit erhalten werden.

Bei der Auswertung nach Habenschaden und Küppers [HAB83] geht man von der logarithmierten Form der Polanyi-Wigner-Gleichung (3) aus. Direkt aus der Auftragung dieser Funktion über der reziproken Temperatur wird hier die Desorptionsenergie mit einer für diese an sich einfache Methode doch beachtlichen Genauigkeit entnommen. Eine Abhängigkeit der Desorptionsenergie von der Bedeckung, dem Frequenzfaktor und der Desorptionsordnung kann vernachlässigt werden, wenn die Thermodesorptionsspektren nur im ersten, kleinen Teil des Anstieges auf der Niedertemperaturseite (bei uns 4%) untersucht werden.

Der große Vorteil dieser Methode ist neben dem geringen Rechenaufwand allerdings der, daß auf Grund des kleinen betrachteten Q-Bereiches, jegliche Wechselwirkung der einzelnen Desorptionszustände ausgeschlossen werden kann. Es ist somit möglich, mit relativ hoher Genauigkeit Desorptionsenergiewerte auch für hohe Bedeckungen zu erhalten. Nachteilig ist allerdings das schwächere Signal-zu-Rausch-Verhältnis der betrachteten kleinen Flankenabschnitte.

4.2.2 Beurteilung der Ergebnisse

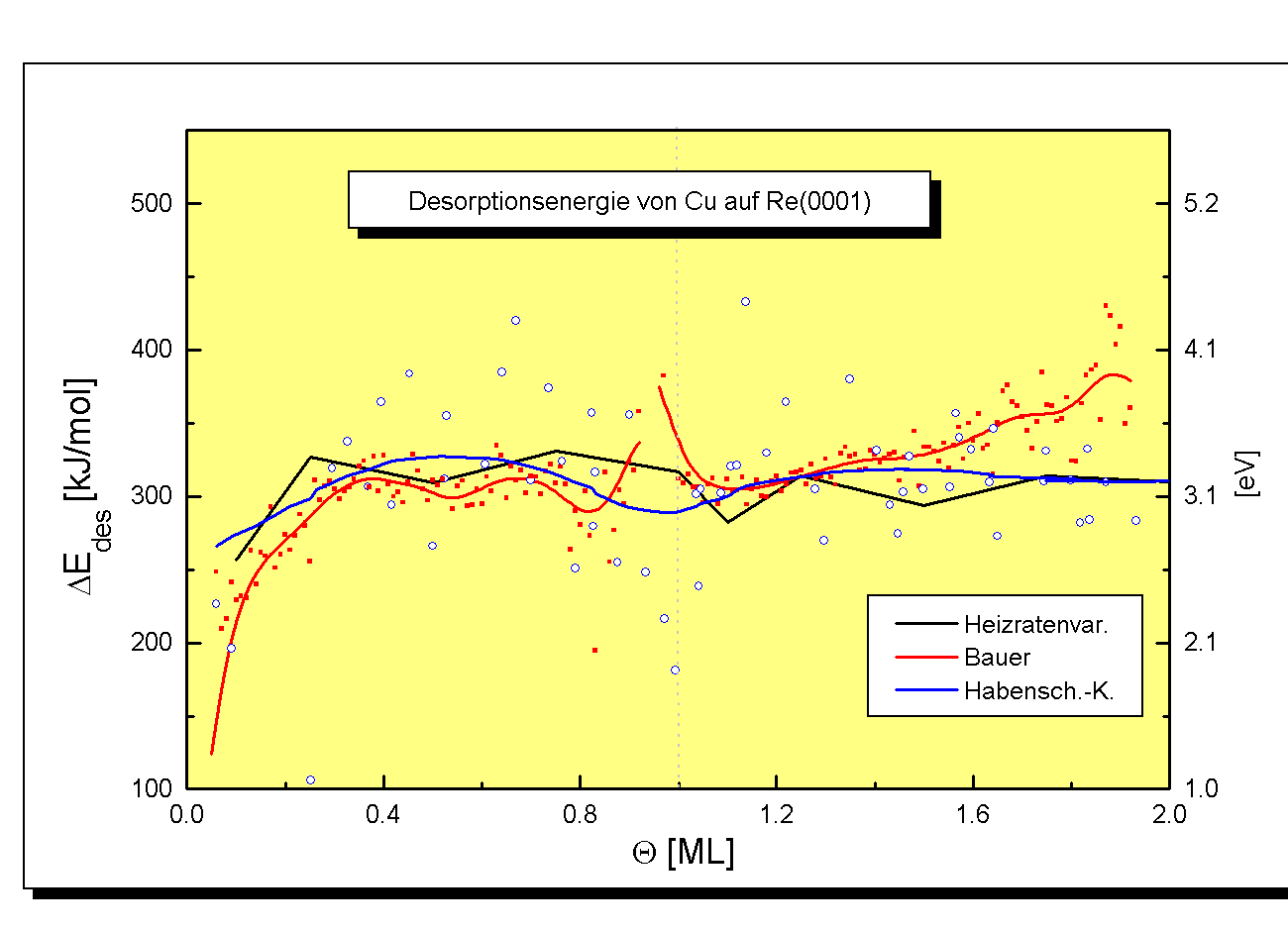Abbildung 12

In Abb.12 ist der Verlauf der Desorptionsenergie als Ergebnis der drei verwendeten Methoden dargestellt.

Im Bereich bis 0,25 ML steigen die zunächst sehr niedrigen Energiewerte mit dem Bedeckungsgrad stark, nämlich von ca. 200kJ/mol auf etwa 310kJ/mol an. Dieser Anstieg der Desorptionsenergie kennzeichnet die Desorption von Teilchen, deren attraktive Wechselwirkungen untereinander mit zunehmenden Bedeckungsgrad größer werden.

Der Bereich von 0,25 ML bis 0,75ML ist durch einen konstanten Wert der Desorptionsenergie von 310kJ/mol gekennzeichnet. Diese Konstanz ist durch die Ausbildung eines zweidimensionalen Phasengleichgewichtes bestimmt [W98/2].

Im Bereich von 0,75ML bis 1ML ist, besonders für die Werte nach Bauer, zunächst ein Abfall um etwa 20kJ/mol und danach ein Anstieg um etwa 80kJ/mol zu verzeichnen. Bei Q=1ML hat sich der Wert von 310kJ/mol wieder eingestellt. Dieser Verlauf, der auch für das Systems Cu/W(110) beobachtet wurde [B75/1], kann auf unterschiedliche Art und Weise diskutiert werden:

• Der Effekt des Abfallens der Kurven kann als Konsequenz morphologischer Ursachen beschrieben werden. Durch die Vollendung der ersten Lage müssen die Adatome immer dichter zusammenrücken und das Mißverhältnis der Gitterkonstanten kommt sehr stark in Form von Spannungen zum Ausdruck. Die Folge davon ist eine Erleichterung der Desorption (Verkleinerung von -DE_des).
• Der Effekt des darauffolgenden Ansteigens kann, wie im ersten Bereich, aus enthalpischer Sicht beschrieben werden. Attraktive Wechselwirkungen der Adteilchen untereinander werden, auf Grund der ansteigender Zahl nächste Nachbarn, maximal.
• Derselbe Effekt läßt sich auch unter Zuhilfenahme des Kompensationseffektes zwischen der Desorptionsenergie und dem Frequenzfaktor, der die Desorptionsentropie beinhaltet, beschreiben. Geht man von der Voraussetzung aus, daß die erste Lage vollständig gefüllt ist, bedeutet dies, daß jedes Adatom vollständig lokalisiert ist. Daraus folgt ein enormer Anstieg der Desorptionsentropie vom Zustand der totalen Ordnung (vollständige Lokalisation auf der Oberfläche) zu einem Zustand totaler Unordnung (Wechselwirkungsfreiheit im (idealen) 3D-Gas). Dafür spricht die für dabei auftretende Frequenzfaktoren (n=10²²s^-1) berechnete Desorptionsentropie in der Größenordnung der Sublimationsentropie des reinen Kupfers.
• Aber auch Wechselwirkungen der einzelnen Lagen untereinander sind möglich [B88/1]. Bevor die erste Lage vollständig aufgefüllt ist, könnten Atome in die zweite Lage eingebaut werden. Bei der Desorption können ebenfalls Atome der ersten Lage desorbieren, bevor die zweite Lage vollständig desorbiert ist. Dies ist z.B. beim System Ag/Re(0001) der Fall, wo allerdings das Adsorbat die größere Gitterkonstante hat [S98/1].

Der gesamte Verlauf korreliert mit den Vorhersagen aus der Diskussion der Arrheniusplots (Abschnitt 4.2.1). Der Anstieg sowie der konstante Verlauf der Desorptionsenergie bis etwa 0,75 ML und von 1ML bis 2ML sind durch die Geradenparameter der Arrheniusplots eindeutig festgelegt. Die starken Änderungen im Bereich von 0,75ML bis 1ML können mit der unterschiedlichen Gewichtung der drei Anstiegsabschnitte der Arrheniusplots erlärt werden. Die Frage, ob man über die unterschiedlichen Anstiege mitteln darf, kann sicherlich nicht endgültig beantwortet werden.

Der Bereich ab 2ML ist durch den konstanten Desorptionsenergiewert (ermittelt duch die Methode nach Habeschaden/Küppers) von 305kJ/mol gekennzeichnet.

5. Diskussion der Ergebnisse

Die Analyse unserer Resultate zeigt, daß sich die kinetischen und thermodynamischen Eigenschaften unseres Systems in mehreren Formen manifestieren. Dies ermöglicht es uns, ausgehend von den Daten der TDS, ein recht umfassendes Bild der Wechselwirkungen von Cu mit Re(0001) zu geben.

1. Es bilden sich bei der Desorption einer genügend dicken Adsorbatschicht drei Desorptionszustände aus. Die beiden Zustände höherer Temperatur b₂ und b₃ sind dabei einzelnen Lagen zuzuordnen, der Zustand niederer Temperatur b₁ verändert seine Form nicht bei der Desorption mehrerer Lagenäquivalente, bezogen auf b₂ und b₃. Dies legt die Vermutung nahe, daß es ab 2ML zur Ausbildung eines dreidimensionalen Wachstums kommt. Die Desorptionsmaxima der Zustände b₁ und b₂ liegen recht nahe beieinander, was sich auch durch eine etwa gleiche Desorptionsenergie manifestiert, s.u.. Der b₃-Zustand liegt energetisch höher, was auf besondere Wechselwirkungen hinweist.

2. Durch verschiedene Analysemethoden lassen sich Aussagen über die Desorptionsordnung treffen und bestätigen.

• Alle drei Desorptionszustände zeigen in den TD-Spektren gemeinsame Anstiegsflanken. Dies ist ein Indiz für eine Desorption nullter Ordnung. Spektren mit Anfangsbedeckungsgraden <0,15ML haben jedoch ein davon abweichendes Verhalten. Deren Desorptionsmaxima liegen bei gleichen Werten, was ein Kriterium für eine Desorptionordnung von eins ist.
• Dieses Verhalten läßt sich auch in den Layerplots, der anderen der beiden Projektionsmöglichkeiten der TD-Pfade über die TD-Fläche, nämlich in die (Q; R)-Ebene beschreiben. Einer Desorption nullter Ordnung ist hier ein konstanter Anstieg im Bereich der höheren Bedeckungsgrade zuzuordnen. Dieses Verhalten zeigen alle Spektren (von allen drei Zuständen) mit einem Anfangsbedeckungsgrad >0,15ML. Der Verlauf der Spektren mit Q₀<0,15ML ist vollständig gekrümmt.
• Die TD-Fläche selbst, in der die drei TD-Zustände gut räumlich getrennt voneinander abgebildet sind, zeichnet sich in bestimmten Bereichen durch in Q-Richtung gerade Abschnitte aus. Diese Abschnitte sind wiederum einer nullten Desorptionsordnung zuzuordnen. Noch besser ist diese Form im konstanten Verlauf der Isothermen zu erkennen.
• Durch eine doppeltlogarithmische Darstellung dieser Isothermen lassen sich auch Aussagen über deren nicht konstanten Teil treffen. Die durch den Anstieg dieser Orderplots bestmmte Desorptionsordnung in diesem Gebiet ist eins. Solche Gebiete bilden sich hauptsächlich zu Beginn und zum Ende der ersten Lage aus. Der Teil dazwischen sowie die Gebiete der anderen beiden TD-Zustände besitzen voneinander getrennte, horizontale Verläufe (n=0).

f) [K96/1] (b=2,4K/s), g) [B87/1], h) [G92/2], i) [S98/1] (b=2,5K/s))

• Für den b₃-Zustand ergibt sich ein Verlauf, der durch starke Unregelmäßigkeiten gekennzeichnet ist. Es kommt hier zur Überlagerung mehrerer Effekte. Der anfängliche Anstieg, der konstante mittlere Verlauf und der Anstieg im Bereich der Auffüllung der Lage können wiederum durch einen zweidimensionalen Phasenübergang beschrieben werden. Der Effekt des Absinkens der Desorptionsenergie bei etwa 0,8ML kann der stärker werdenden Misfit-Gitteranpassung zugeordnet werden. Ähnliche Verläufe finden Bauer et al und Gollish et al für die Systeme Cu/W(110) und Cu/Mo(110). Die mittleren Desorptionsenergiewerte liegen vor allem für die W-Oberfläche höher, was durch eine stärkere elektronische Wechselwirkung erklärt werden kann. Für das System Ag/Re(0001) wird ein Wert von 293kJ/mol angegeben [S98/1]. Silber hat zwar eine ähnliche Elektronenkonfiguration wie Kupfer, jedoch ist sein Atomradius von r=1,44Å größer als der von Rhenium r=1,38Å. Natürlich stimmt auch der Radius des Kupferatoms r=1,28Å [WEA74] nicht mit dem des Rheniums überein, doch ist auf Grund der Fehlanpassung zugunsten des Silbers eher von einer stärkeren Wechselwirkung auszugehen, die zu einer Lockerung der Bindung zum Substrat führt. Daraus resultiert die niedrigere Desorptionsenergie. Auch der Effekt des Anstieges der Desorptionsenergie im Bereich hoher Lagenbedeckungen wird warscheinlich durch den Misfit überdeckt. Der Literaturwert von 389kJ/mol für die Desorptionsenergie von Cu auf Re(0001) [G92/1, G90/2] weicht erheblich von unserem Wert ab. Das rührt daher, daß dort nach dem Verfahren von Polanyi , was natürlich Schwächen aufweist, gearbeitet wurde. Außerdem sind diese Spektren mit einer sehr hohen Heizrate aufgenommen worden, was die ‘Deutlichkeit’ der Kurven beeinträchtigt. Es wurde weiterhin auch kein Kurvenverlauf angegeben, sondern nur ein (warscheinlich gemittelter) Wert.
• Im Bereich der b₁- und b₂-Zustände ist die Desorptionsenergie etwa konstant. Dies steht in guter Übereinstimmung mit den Literaturwerten, s.o.. Auch der Literaturwert von He et al [G90/2, G92/1] (310kJ/mol) für Cu/Re(0001) stimmt mit unserem Meßwert überein. Die Wechselwirkungen des Substrats mit dem Adsorbat haben im Bereich der zweiten Lage bereits merklich nachgelassen, was man einerseits an den fehlenden (bzw. sehr schwachen) Unregelmäßigkeiten im Verlauf der Desorptionsenergie erkennen kann, andererseits an der Übereinstimmung der Desorptionsenergie für die beiden Zustände.

6. Literaturverzeichnis