Energetik und Kinetik des Systems Cu/Re(0001) - Diplomarbeit von Ronald Wagner

3. Weiterführende Untersuchungen

In diesem Abschnitt sollen einige weiterführende (allerdings kurze) Überlegungen zur Entropie der Desorption angestellt werden. Danach wird ausführlicher auf das sich ergebende Phasengleich-gewichtsverhalten des Systems Cu/Re(0001) eingegangen sowie eine Methode vorgestellt, mit deren Hilfe Aussagen zu Phasenparametern wie der kritischen Temperatur T_c gewonnen werden. Weiterhin wird die interne Wechselwir-kungsenergie der Adsorbatteilchen E_WW bestimmt.

 3.1 Schlußfolgerungen für die Desorptionsentropie

DS_des kann als negative Adsorptionsentropie angesehen werden. Sie ist die Differenz der Entropie der (3D-) Gasphase und der Gesamtentropie des Systems Substrat/Adsorbat. Da die Entropie der (als ideal angesehenen) Gasphase stets die größere ist, ist DS_des immer positiv. Eine hohe Desorptionsentropie kennzeichnet also eine kleine Entropie des Adsorptionssystems und damit einen hohen Ordnungszustand auf der Oberfläche.

Nach Gleichung (14) ist die Desorptionsentropie mit dem Frequenzfaktor exponentiell verknüpft. (n ist der sich aus den Rechnungen ergebende Frequenzfaktor, der noch die Heizrate beinhaltet.)

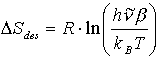(59)

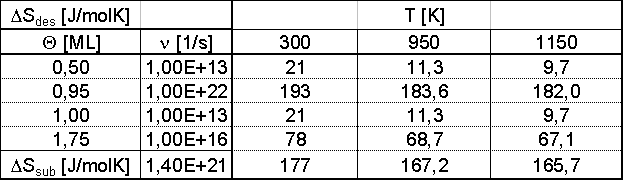
Tabelle 5 Desorptionsentropie, Sublimationsentropie nach [WEA71]

Der Verlauf der Desorptionsentropiekurve bei einer vorgegebenen Temperatur ist also bis auf einen Faktor derselbe wie der von lgn. Im Bereich bis etwa 0.2ML steigt DS_des bis auf einen konstanten Wert von etwa 10,5J/(molK) an. Im ersten Bereich sind die Teilchen noch sehr beweglich, d.h. sehr ungeordnet. Der Entropiegewinn beim Übergang ins 3D-Gas ist nicht sehr groß. Im Bereich der Koexistenz 2D-Gas/Kon-densat muß der Übergang vom Kondensat ins 2D-Gas berücksichtigt werden. Dabei bleibt die Desorptionsentropie konstant auf einem mittleren Wert. (Kurz vor dem Abschluß der ersten Lage wird sie sehr groß, da der Ordnungszustand der jetzt vollständig kondensierten und lokalisierten Phase maximal ist.) Die einzelnen Werte der Desorptionsentropie bei Raumtemperatur (hier ist zur Umrechnung ein konstanter Verlauf der Molwärme mit der Temperatur approximiert worden) und bei den Temperaturen zu Beginn und zum Ende der Desorption sind in Tab. 5 gegeben.

 3.2 Mikroskopische Betrachtungen

3.2.1 Das Modell des zweidimensionalen Gases

Eventuell etwas vorgreifend auf die Erkenntnisse der folgenden Ausführungen soll, bezugnehmend auf Kapitel I.2.1.3 (Das Modell des zweidimensionalen Gases), zunächst das verwendete Modell genau beschrieben werden. Das betrachtete System besteht aus einer Substratoberfläche (Re(0001)), die eine genau definierte Anzahl von Adsorptions-plätzen N besitzt. Auf dieser Oberfläche befinden sich, je nach Verlauf der Adsorption eine bestimmte Anzahl von Adsorbatteilchen (Cu-Atome).

Diese gehen Wechselwirkungen mit dem Substrat ein (gekennzeichnet durch die Adsorptionsenthalpie DH_ads), aber sie können auch mit ihren nächsten Nachbarn, in Abhängigkeit ihrer Oberflächenkonzentration Interaktionen ausbilden (bestimmt durch die interne Wechselwirkungsenergie E_WW).

Es wird davon ausgegangen, daß sich die Teilchen nur in einer Monolage befinden und eine zweite Lage nicht ausgebildet wird. Damit kann man die Gesamtoberflächen-konzentration durch die Bedeckung dieser Lage Q_ML ausdrücken. Diese Größe kann maximal eins sein, d.h. jeder Adsorptionsplatz ist durch genau ein Teilchen besetzt.

Betrachtet wird (durch Thermodesorptionsspektroskopie) der Vorgang der durch thermische Energie k_BT induzierten Desorption in einem Temperaturbereich vom Einsetzen bis zum Abklingen des Vorganges (etwa 950K bis 1200K). Zu Beginn der Desorption ist die Bedeckung gleich der Anfangsbedeckung Q_ML=Q₀ und nimmt während des Prozesses ab, bis kein Teilchen mehr auf der Substratoberfläche vorhanden ist. Die Energie, die aufgebracht werden muß, damit ein (Mol) Teilchen desorbiert, ist die Desorptionsenergie DE_des.

Auf der Oberfläche bilden sich, je nach Bedeckung ein oder zwei Phasen aus. Bei geringen Bedeckungen befinden sich alle Teilchen in der Phase des 2D-Gases und können sich frei (vom Potential in x- und y- Richtung) auf der Oberfläche bewegen. Für Q_ML®0 besitzen die Adsorbatteilchen ideale Gaseigenschaften, die durch zunehmende Bedeckung und damit verbundene vermehrte interne Wechselwirkungen abklingen. Ab einer bestimmten Bedeckung Q_g,u (bei der niedrigsten Desorptionstemperatur, 950K) werden die Wechselwirkungen wegen des zu geringen Platzangebotes so stark, daß eine zweite Phase gebildet wird, die aus kondensierten Teilchen besteht. Diese bilden Inseln auf der Oberfläche aus, zwischen denen sich weiterhin 2D-Gasteilchen bewegen können. In dieser Koexistenzregion, die zu hohen Temperaturen begrenzt ist (bei der kritischen Temperatur T_c), stehen die beiden Phasen im Gleichgewicht.

In dieser Region ist die Konzentration der Teilchen in beiden Phasen konstant. Die 2D-Gaskonzentration entspricht derjenigen bei Q_g,u und die der kondensierten Phase ist stets eins. Die gebildeten Inseln sind also in sich kompakt, was nichts über ihre äußere Form aussagt. Die Bedeckung mit kondensierten Teilchen Q_c kann sich jedoch durch die Veränderung von Anzahl und Größe der Inseln ändern. Äquivalent (nach Q_ML=Q_c+Q₂) kann sich bei konstanter Konzentration mit 2D-Gasteilchen auch die Bedeckung durch diese Teilchen Q₂ ändern.

Die Desorption erfolgt stets aus der 2D-Gasphase, die jedoch durch das o.a. vorgela-gerte Gleichgewicht sofort nachgebildet wird, so daß ihre Konzentration konstant bleibt, solange die kondensierte Phase vorhanden ist.

Bei Q_ML®1 ist nur noch die kondensierte Phase vorhanden, da jeder Adsorptionsplatz von einem Teilchen besetzt ist.

Wie unter 1.3.1 ausgeführt ist die Ausbildung einer gemeinsamen Anstiegsflanke der Thermodesorptionsspektren ein Zeichen für eine Desorption nullter Ordnung. Die Temperatur T_g, bei der die Flanken der einzelnen Spektren Abweichungen von der gemeinsamen Anstiegsflanke zeigen, kennzeichnet den Übergang von der Koexistenz-region 2D-Gas/Kondensat zu der reinen 2D-Gasphase [NAG86], (vgl. I.3.1.10). Die Desorptionsrate steigt ab dieser Temperatur nicht mehr so stark an wie davor (s. z.B. Abb.37). Dieser Effekt wird durch die Konzentrationsabnahme der Teilchen im 2D-Gas ausgelöst.

Die Spektren der kleinsten Anfangsbedeckungen (Q₀<0.1ML) besitzen, wie schon oben ausgeführt, keine gemeinsame Flanke. Das bedeutet, daß bis zu dieser Bedeckung nicht von einer Bedeckungsgradunabhängigkeit der Desorptionsrate ausgegangen werden kann.

3.2.2 Das Phasendiagramm

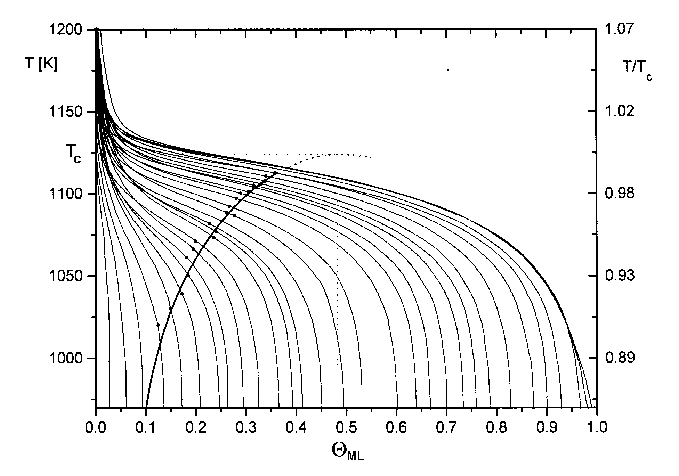
Abbildung 50 Phasendiagramm für das System Cu/Re(0001)

Es soll hier eine einfache Möglichkeit vorgestellt werden, um aus den Daten einer Serie von Thermodesorptionsspektren in einem T(Q)-Diagramm die Phasengrenze 2D-Gas/2D-Gas-Kondensat bis etwa zur kritischen Bedeckung Q_c zu erhalten. Am Beispiel des b₃-Zustandes (1.Monolage) ist dies durchgeführt worden (s. Abb.50).

Jedem Spektrum innerhalb der Serie wird dazu als erstes das Wertepaar (Q₀; T_g) entnommen. Als zweites werden die Spektren von der Hochtemperaturseite her integriert, um den Verlauf der Bedeckungsgrade mit der Temperatur Q_ML=ƒ(T) zu erhalten. Die Serie der integrierten Thermodesorptionsspektren wird dann invers, also in der Form T=ƒ(Q_ML) dargestellt.

Auf den so entstandenen Desorptionslinien (die die Abhängigkeit der Desorptions-temperatur vom Bedeckungsgrad für die Desorption ausgehend von einer bestimmten Anfangsbedeckung Q₀ darstellen) wird jeweils das Wertepaar (Q₀; T_g) eingetragen. Durch die so erhaltenen Punkte kann das Wertepaar zum Wertetripel (Q₀; T_g; Q_g) erweitert werden, indem man die zu T_g gehörige Phasengrenzbedeckung dem Diagramm entnimmt. Außerdem können die Punkte zu einer Linie verbunden werden, die die Phasengrenze 2D-Gas/Koexistenzregion markiert.

Die Phasengrenzlinie kann so natürlich nur bis zu dem Punkt erhalten werden, an dem die Desorptionslinien die Phasengrenze durchschneiden. Um die kritische Temperatur T_c und die kritische Bedeckung Q_c zu erhalten, wird berücksichtigt, daß im Bereich der Auffüllung der Monolage die Phasengrenze die Q_ML-Achse wieder schneidet. Bei Q_ML=1 kann keine Koexistenzregion mehr vorhanden sein, da alle Teilchen kondensiert vorliegen (s.o.). Extrapoliert man den Kurvenverlauf unter Berücksich-tigung dieses Umstandes weiter, erhält man das Maximum der Kurve, dessen Koordinaten die kritischen Werte sind.

Aus Abb.50 wurden folgende Werte entnommen: T_c=1120K, Q_c=0,48ML. Als Literaturwerte wurden für das System Cu/W(110) T_c=1150K und Q_c=0,215ML [BAU85] sowie für das System Cu/Mo(110) T_c=1148K [BAU87] gefunden. Diese Punkte liegen weit außerhalb der Koexistenzregion aus Abb.50. In den von Bauer betrachteten Systemen ist diese Koexistenzregion also größer. Das ist auch verständlich, da dort, wie schon unter 1.4.6.a ausgeführt, die Wechselwirkungen stärker sind und sich in einem größeren Bereich des Phasendiagramms eine Region ausbilden kann, die z.T. aus kondensierten Teilchen besteht.

 3.2.3 Weitere Parameter

Nach [NAG84] und [BAU87] ist es (unter Anwendung der Molekularfeldnäherung) möglich, aus der kritischen Temperatur die Wechselwirkungsenergie E_WW der Adsorbat-teilchen untereinander zu bestimmen.

(60)

Der so errechnete Wert beträgt E_WW=6,2kJ/mol. Das sind 2% der Desorptionsenergie. (Nach Gleichung (29) ergibt sich bei Nichtberücksichtigung dieses Wertes bei der Desorptionsenergieauswertung ein Fehler von 6%.) Folgende Literaturwerte wurden für ähnliche Systeme gefunden: Cu/W(110) E_WW=7,9kJ/mol [BAU85] und Cu/Mo(110) E_WW=7,6kJ/mol [BAU87].

Als ein weiterer Parameter wurde die untere Grenzbedeckung (T=950K) Q_g,u»0,1bestimmt. Das ist die Bedeckung, bei der die Desorptionslinien ausschließlich im 2D-Gasphasengebiet liegen, bzw. die Anfangsbedeckung, bis zu der die Thermo-desorptionsspektren überhaupt nicht in der gemeinsamen Anstiegsflanke der Spektren zu höheren Anfangsbedeckungen laufen.

Diese Bedeckung ist aus Abb.50 nur mit geringer Genauigkeit zu entnehmen. Eine Erhöhung der Genauigkeit zur Bestimmung der Grenzbedeckung wird durch die Verwendung der Darstellung der Desorptionsrate vs. Bedeckungsgrad (vgl. 1.2) erreicht. Hier können mit dem Wertepaar (Q₀; Q_g) wiederum Punkte bestimmt werden, die zu einer Linie verbunden werden.

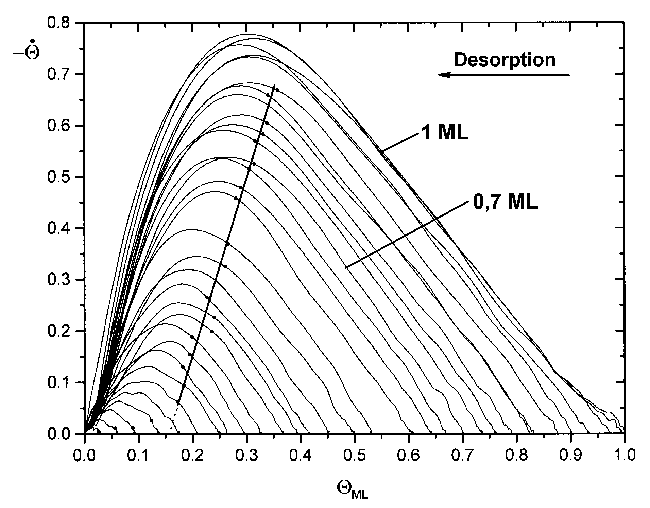
 Abbildung 51 Bestimmung der unteren Phasengrenzbedeckung

Diese Linie zeigt in einem weiten Bereich, nämlich zwischen 0,17 und 0,35 einen konstanten Anstieg. Der physikalische Hintergrund kann unter Zuhilfenahme der Polanyi-Wigner-Gleichung erläutert werden.

(10)

Der konstante Anstieg der Linie in Abb.51 kennzeichnet die Temperaturabhängigkeit der Phasengrenzbedeckung Q_g und damit auch das Phasengleichgewicht zwischen reiner 2D-Gasphase und der Koexistenzregion. Der eigentlich exponentielle Anstieg der Phasengrenzbedeckung mit der Temperatur ist durch die besondere Auftragung Desorptionsrate vs. Bedeckungsgrad in Abb.51 zu einer linearen Funktion gestreckt worden (wie man aus (10) entnehmen kann ().

Extrapoliert man den konstanten Verlauf der Kurve auf die Q-Achse, erhält man mit großer Genauigkeit den Wert von Q_g,u. Für das hier betrachtete System ist Q_g,u=0,16. (Dieser Wert wurde auch schon aus Abb.31a erhalten.)

Um Abb. 51 genau verstehen zu können, muß man bedenken, daß in der Darstellung von rechts nach links der Verlauf der Desorption beschrieben wird. Dem Diagramm kann die Desorptionsrate zum momentanen Bedeckungsgrad für eine Desorption, ausgehend von einer bestimmten Anfangsbedeckung entnommen werden.

Die Abschnitte der Desorptionslinien, die im Bereich der Koexistenzregion 2D-Gas/Kondensat, also im rechten Teil der Darstellung laufen, zeigen ebenfalls einen konstanten Anstieg. Geht man von Gleichung (10) aus, sollte die Desorptionsrate für eine Desorption nullter Ordnung (wie für die Koexistenzregion konstatiert) durch n=0 konstant sein. Das dies nicht der Fall ist rührt daher, daß sich die Desorptionsordnung auf die Konzentration der desorbierenden Komponente bezieht, die Abszisse der Darstellung jedoch die Gesamtbedeckung ist.

Wir haben die Vorstellung, daß die Teilchen nur aus der (stets und instantan nachgebildeten) 2D-Gas-Komponente der Koexistenzregion heraus desorbieren. Die Desorptionsordnung ist dann allein abhängig von der Konzentration dieser 2D-Gasteilchen und bleibt solange konstant null, wie Teilchen aus der kondensierten Komponente mit einer hohen Geschwindigkeit in 2D-Gasteilchen überführt werden, also das Phasengleichgewicht eingestellt bleibt. Betrachtet man jedoch die Gesamtbe-deckung, so ist natürlich die Desorptionsordnung keineswegs konstant, sondern ändert sich abhängig davon, ob das Gleichgewicht erhalten bleibt oder nicht.

 3.2.4 Kinetik der Desorption

Wir können die Kinetik der Vorgänge auf der Substratoberfläche über ein Schema approximieren, das die Desorption als eine Reaktion mit vorgelagertem Gleichgewicht beschreibt.

Als Reaktionsgleichung für diese Reaktion gilt:

(61)

n_c2 ist der Frequenzfaktor für den Übergang von kondensierten Teilchen zu 2D-Gasteilchen, n₂ ist der Frequenzfaktor für die Desorption aus der 2D-Gasphase, C=Teilchen der kondensierten Phase, 2 =Teilchen der 2D-Gasphase und 3D=Teilchen der 3D-Gasphase.

Um die Vorgänge bei der Desorption besser verstehen zu können, betrachten wir zunächst den Fall a) der isothermen Adsorption und danach den Fall b) der Desorption ausgehend von bestimmten Anfangsbedeckungen.

In Abb.52 sind die beiden Prozesse dargestellt, nämlich die isotherme Adsorption von links nach rechts und die Desorption von rechts nach links. Als Abszisse ist die Gesamtbedeckung gewählt. Auf der linken Achse ist die (auf die Maximalbedeckung bei Adsorptionstemperatur) normierte Bedeckung mit 2D-Gasteilchen abgetragen, die rechte Achse gibt die Summe der Bedeckung mit 2D-Gasteilchen und kondensierten Teilchen an.

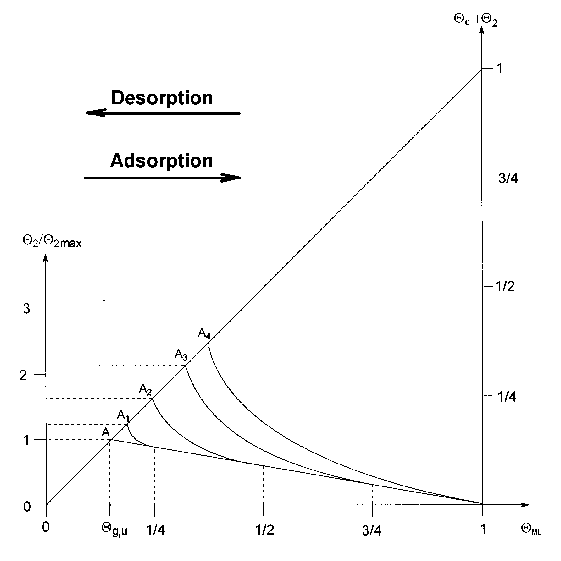
Abbildung 52 Konzentration der Komponenten des 2D-Gasmodells

a) Isotherme Adsorption:

Anhand von Abb.51 haben wir gesehen, daß bei der Adsorption im Bereich bis Q_g,u(=0,16) alle Teilchen als 2D-Gasteilchen vorliegen. Ehe Q_g,u erreicht ist, nimmt die Dichte der Teilchen stetig zu. Der Ausdruck für den Frequenzfaktor der Desorption aus der 2D-Gasphase (Gleichung (22)) kann also so nur für den Fall Q®0 gelten. Bei Q_g,u wird n₂=n_c, so daß der Ausdruck für den Frequenzfaktor der Desorption aus der kondensierten Phase n_c (Gleichung (24)) für die Desorption aus der dichtesten 2D-Gasphase (bzw. für die Desorption aus der 2D-Gaskomponente der Koexistenzphase) ebenso gilt.

Wird Q_g,u überschritten (A), führt eine weiter steigende Bedeckung zur Ausbildung und Erhöhung des Anteils der kondensierten Phase; wir erhalten die Koexistenz-region 2D-Gas/Kondensat. Durch den steigenden Anteil der kondensierten 2D-Phase wird der dem 2D-Gas zur Verfügung stehende Raum kleiner, deshalb verringert sich auch bei konstanter Gasdichte der Flächenanteil dieser Spezies. Im Extremfall, bei Q_ML=1 sind gar keine 2D-Gasteilchen mehr vorhanden, da für jedes Teilchen genau ein Adsorptions-platz zur Verfügung steht.

Wir sehen also, daß die Kurve, die den 2D-Gasanteil beschreibt, zunächst linear bis zum Punkt A ansteigt, dann aber ebenso linear wieder abnimmt.

b) Desorption (zu bestimmten Q₀):

In Abb.52 sind die Desorptionslinien für die Desorption von fünf verschiedenen Anfangsbedeckungen eingetragen (Q₀=1ML; 0,75ML; 0,5ML; 0,25ML; 0,16ML). Diese durchlaufen die Punkte A₄ bis A.

Wir beginnen mit einer bestimmten Anfangsbedeckung (z.B. Q₀=1ML) und betrachten die 2D-Gasbedeckungsänderung als Funktion der (wegen der linearen Temperatur-erhöhung) abnehmenden Gesamtbedeckung.

Die Desorption besteht, außer für den Fall Q_ML=1, einzig aus dem Übergang von 2D-Gasteilchen in die 3D-Gasphase. Interessant ist, daß sich dabei die Bedeckung durch 2D-Gasteilchen zunächst (bis Q_g) vergrößert. Die Desorption beinhaltet den umge-kehrten Prozeß der isothermen Adsorption. D.h., durch die Desorption verringert sich die Konzentration der 2D-Gaskomponente deshalb nur scheinbar, weil sofort Teilchen der kondensierten Komponente zu 2D-Gasteilchen nachreagieren. Der Raumbedarf der kondensierten Komponente wird dabei geringer, und so werden noch mehr 2D-Gasteilchen gebildet. Als zusätzlicher Effekt tritt die stärkere Beweglichkeit der Teilchen bei höherer Temperatur auf (die Temperatur wird ja gerade bei der Thermodesorption linear erhöht). Dadurch treten, nach dem in Abb.50 erkennbaren exponentiellen Zusammenhang zwischen Bedeckung und Temperatur, mehr konden-sierte Teilchen in die 2D-Gaskomponente über. Bei den Punkten A₁ bis A₄ liegen, je nach Anfangsbedeckung (A₄ für Q₀=1ML), ausschließlich 2D-Gasteilchen vor.

Während des Prozesses erhöht sich zwar die Bedeckung mit 2D-Gasteilchen, die Dichte dieser Komponente und damit die die Reaktionsordnung bestimmende Konzentration bleibt jedoch konstant. Daraus erklärt sich der Wert n=0.

Nachdem die Desorption die Punkte A_n durchlaufen hat, verringert sich schließlich sowohl die Bedeckung durch die 2D-Gasteilchen als auch deren Konzentration, und die Desorptionordnung ist hier n=1.