Kapitel A1	Abschnitt A - Theoretische Grundlagen
		Kapitel A3	Kapitel A2 - Metall-Epitaxie

2. Metall-Epitaxie

Aus den zwei griechischen Wörtern e p i (epi – darüber) und t a x i z (taxis – angeordnet) wurde das Wort Epitaxie gebildet, welches ein sehr wichtiges Phänomen beim Wachstum dünner Filme beschreibt, die orientierte Substratabscheidung [Neu51/1]. Es charakterisiert die Entstehung von ausgedehnten Filmen auf einem kristallinen Substrat, wobei beide Kristallarten weder isomorph noch isotyp sein müssen.

Bereits die Morphologie dünnster Adsorbatschichten kann für die Struktur dickerer Filme ausschlaggebend sein. Zum Wachstum von dünnen Filmen eignen sich deshalb definierte (Ein-) Kristalloberflächen besonders, weil sie dem Film schon während der Entstehung wichtige Strukturinformationen aufprägen können.

Es werden zwei Arten der Epitaxie unterschieden, nämlich Homo- und Heteroepitaxie. Homoepitaxie beschreibt das Wachstum von Filmen der gleichen Atomart wie die der Unterlage. Diese Art des Wachstums kann als relativ ideal angesehen werden, da es sich hierbei um ein Fortführen des Kristallaufbaus handelt. Trotzdem treten auch hier Effekte auf, die eine 100%-ige Weiterführung der Kristallmorphologie hemmen können.

Bei der Heteroepitaxie handelt es sich um das Wachstum von Filmen einer anderen Atomart als der des Substrates. Zusätzlich zu den Effekten, die beim homoepitaktischen Wachstum auftreten, kommt es hier zu einer Vielzahl von Phänomenen, wie z. B. Verspannungen in der obersten Substrat- oder in den Adsorbatlagen, Rekonstruktionen der Oberfläche oder Legierungsbildungen, um nur einige zu nennen.

Wissenschaftler haben sich häufig mit epitaktischen Systemen befaßt. Umfangreiche Übersichtsartikel zu diesem Thema sind in der Literatur zu finden, z. B. von Rodriguez [Rod96/1], Brune [Bru98/1], Bauer [Bau58/1, Bau58/2, Bau82/1], Zinke-Allmang [Zin99/1], Hwang und Behm [GGK93/1].

 

A.2.1 - Keimbildung

 

2.1. Keimbildung

Der erste Schritt zur Entstehung eines epitaktischen Filmes ist das Aufbringen bzw. die Ablagerung eines bzw. mehrerer Adsorbatteilchen (Adatome) mit nachfolgender Keimbildung (Nukleation). Der dazu nötige Materialtransport kann auf unterschiedliche Weise geschehen.

 

A.2.1.1 - Segregation

 

2.1.1. Segregation

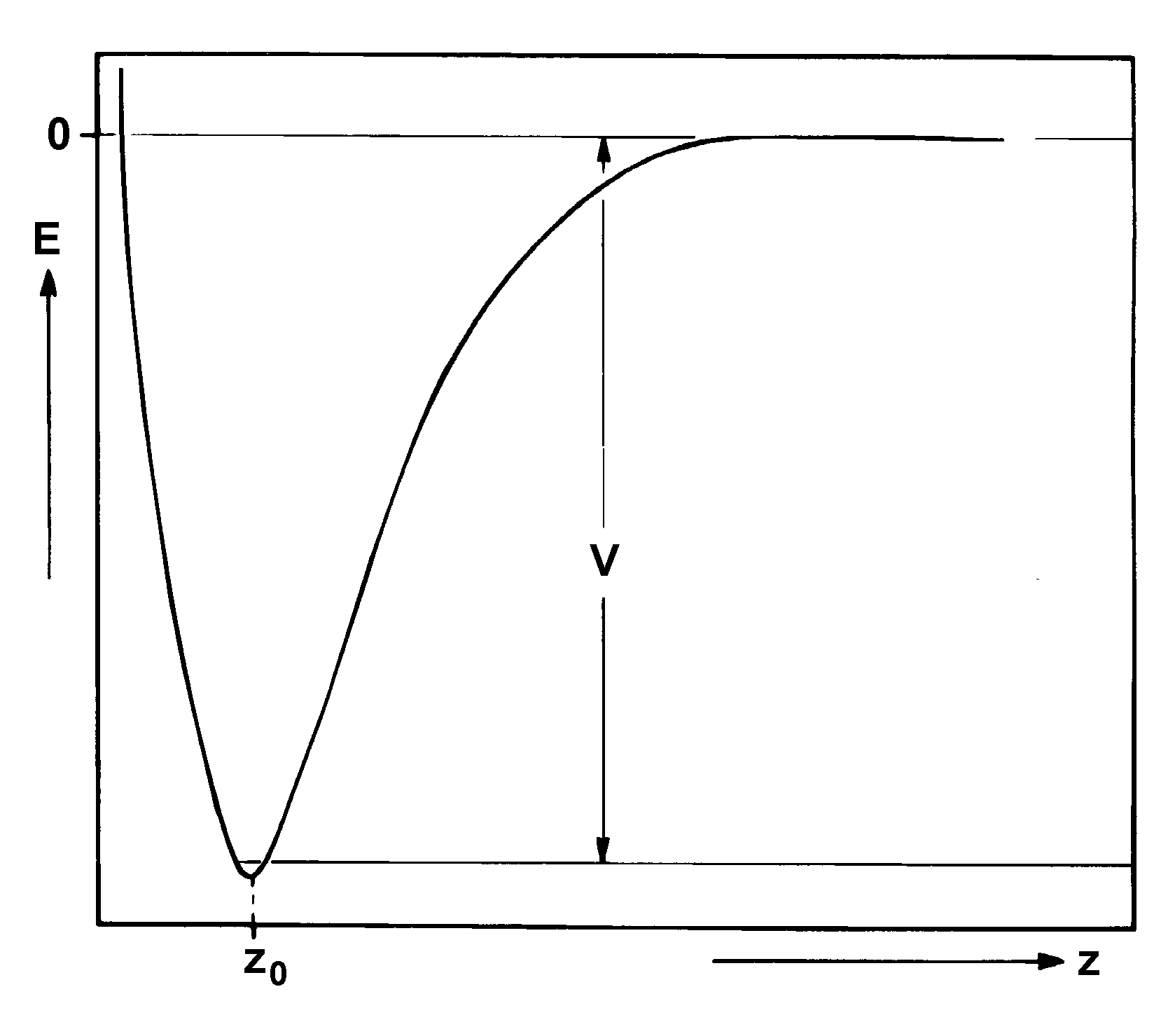
Abbildung A3  Bindungspotential für ein chemisorbiertes Teilchen nach [Chr91/b]

Stammt das Adatom aus der Unterlage, so spricht man von Segregation, die z. B. thermisch aktiviert sein kann.

Dabei kann ein Teilchen durch Temperaturerhöhung aus dem Volumen an die Oberfläche, die dadurch relaxieren könnte, emporgehoben werden.

Bei heteroepitaktischem Wachstum wäre ein solcher Prozeß etwa aus einer Legierung denkbar (insbesondere bei Teilchen, deren Oberflächenenergie kleiner als diejenige des Substrates ist [ESJ94/1]) und könnte zur Verarmung des Oberflächenbereiches an der einen und zur Anreicherung der anderen Atomart führen. Der Segretationsgrad hängt weiterhin von der Mischungsenthalpie und -entropie sowie vom Radienverhältnis der beteiligten Stoffe ab. Beispiele für segregierende Volumenlegierungen sind PdX mit X = Cu, Ni, Co, Fe [Rod96/1].

 

A2.1.2 - Abscheidung aus der Gasphase

 

2.1.2. Abscheidung aus der Gasphase

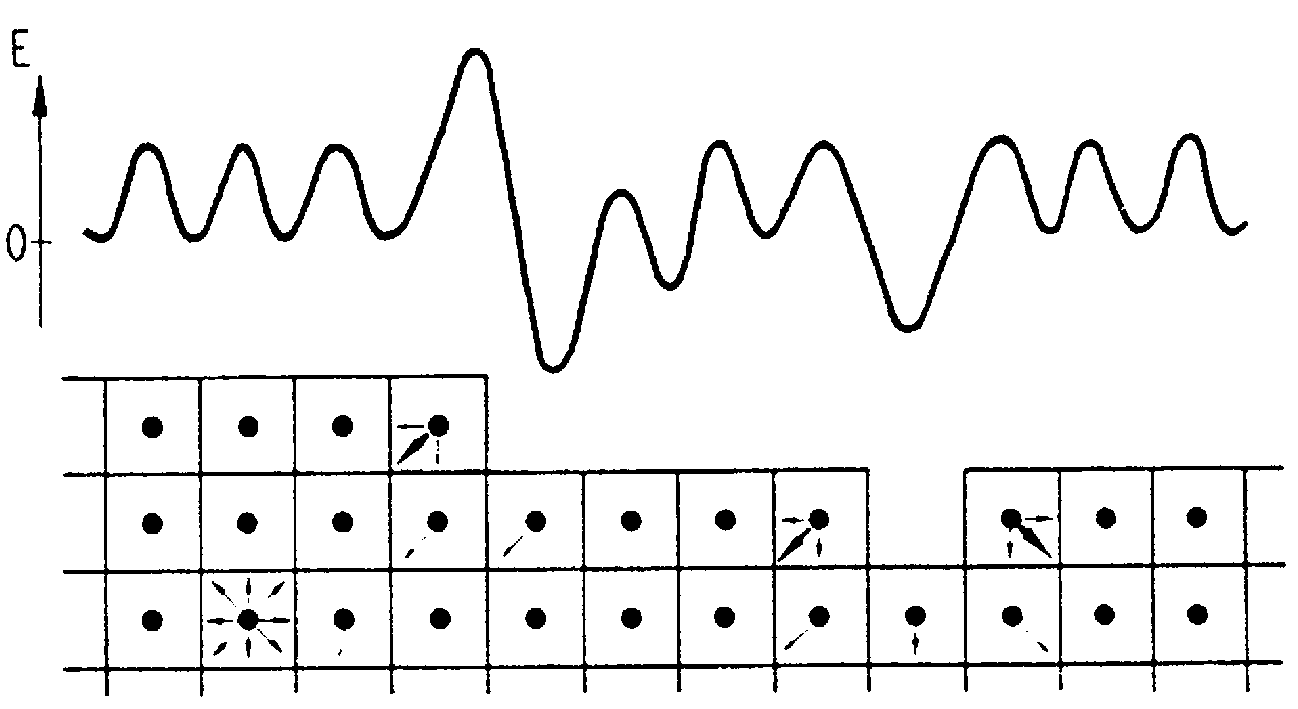
Abbildung A4  Diffusionspotential für Adteilchen auf einer Oberfläche mit Stufen, Terrassen und Vakanzen, nach [Wan91/1].

Eine zweite Möglichkeit, wie Teilchen auf die Oberfläche gelangen können, ist insbesondere bei Metallen das Aufdampfen (das Auftreffen eines gerichteten Atomstrahls), oder indem die Oberfläche einer bestimmten Atmosphäre des Adsorbatgases ausgesetzt wird. Ein aus der Gasphase auftreffendes Teilchen spürt dabei ein Multipotentialfeld, das aus Dipol- und aus kovalenten Wechselwirkungen zum Substrat und/oder zu anderen bereits vorhandenen Adteilchen besteht, s. Abb. A 3. Die Energie, die das Teilchen auf Grund seiner Bewegung in der Gasphase besitzt, muß es nach Auftreffen auf der Oberfläche rasch abgeben, damit es nicht wieder desorbiert. Diese Energie wird im Allgemeinen vom Substratgitter (oder einer evtl. bereits vorhandene Adsorbatlage) aufgenommen. Das Teilchen kann aber auch einen Teil der Energie behalten und sich dann auf der Oberfläche bewegen. Auch hierbei ist es einem Potential ausgesetzt, das besonders an bestimmten Adsorptionsplätzen (etwa Muldenplätzen) bindend ist, aber auch Diffusionsbarrieren, z. B. an on top-Plätzen, aufweist, vgl. Abb. A 4. Die Tiefe dieser Potentialmulden ist meist etwa 1/10 der Bindungsenergie der Adteilchen. Hexagonal dicht gepackte Flächen besitzen sehr kleine Diffusionsbarrieren, im Gegensatz zu tetragonalen dicht gepackten oder offenen Flächen [Bru98/1]. Bei Metall/Metall-Systemen kann eine sehr große Beweglichkeit der Adteilchen bereits unterhalb von Raumtemperatur vorliegen.

2.2. 1D- und 2D-Wachstum

2.2.1. Entstehung von Inseln

Nachdem der Prozeß der Keimbildung abgeschlossen ist, schließt sich (teilweise nach Durchlaufen eines Übergangszustandes) das Wachstum von Inseln an, wie besonders Brune anhand des Systems Ag/Pt(111) überzeugend demonstrierte [Bru98/1]. Der Übergang zwischen diesen beiden Prozessen läßt sich damit erklären, daß Teilchen und cluster, die noch nicht die CCS besitzen, viel häufiger mit stabilen Keimen zusammenstoßen als mit anderen frei beweglichen Teilchen oder nicht stabilen Keimen [BRB94/1]. Beim Wachstum von großen Inseln kommt es zusätzlich zur Ausbildung einer Verarmungszone mit clustern subkritischer Größe, was beim Zusammenstoßen solcher Zonen darin gipfeln kann, daß gar keine Keimbildung mehr möglich ist.

 

A2.2.2 - Inselformen

 

2.2.2. Inselformen

Die Formen der gebildeten Inseln können stark variieren und hängen von der Substrat- und Adsorbatmorphologie, von der Substrattemperatur und von der Nukleationsrate ab. Eindimensionale (1D-) Strukturen bilden sich bevorzugt bei anisotropen, z. B. gestuften Oberflächen und sind immer metastabil, wie beispielsweise im Fall des Cu/Pd(110) [Rod96/1] oder Ag/Re( 1 0  1 ¯  0 ) bzw. Au/Re( 1 0  1 ¯  0 ) [Vol99/d]. In der Mehrzahl der Fälle bilden sich jedoch von Beginn an zweidimensionale (2D-) Inseln aus.

Das Verhältnis zu Diffusions- und Nukleationsrate ist hierbei sehr wichtig [BaC95/1, BaS01/1, HZK99/1, HZK01/1]. Ist dieses Verhältnis klein (etwa bei einer hohen Aufdampfrate und niedriger Substrattemperatur), kommt es zum diffusionsratenbestimmten Wachstum (diffusion limited aggregation, DLA). Dies führt dann zur Ausbildung von verzweigten Inseln, die zufällige dendritische Formen haben (Pt/Pt(111), 180 K [Bru98/1]) oder (durch substratorientiertes Wachstum) symmetrische Fraktale bilden (Pt/Pt(111), 300 K [Bru98/1], Au/Ru(0001) [Rod96/1]). Ist das o. a. Verhältnis groß oder werden dendritische Inseln erhitzt, kommt es wegen Relaxationen an den Inselrändern zur Bildung von kompakteren Inseln (Pt/Pt(111), >  400 K [Bru98/1]). Zwischen diesen beiden Grenzfällen besteht ein fließender Übergang.

Die Rolle der Substratstruktur im Hinblick auf das fraktale oder kompakte Wachstum ist als eher groß bei erhöhten Temperaturen und als eher gering bei niedrigen Temperaturen einzuschätzen [HZK99/1, HZK01/1]. Dabei ist entscheidend, daß bei höheren Temperaturen die Adteilchen auf Grund der vergrößerten Diffusionsfähigkeit die Möglichkeit erhalten, energetisch günstige Plätze einzunehmen. Auf tetragonalen Flächen ist es günstiger, eine kompakte Inselform auszubilden, da es im Gegensatz zu Inseln auf hexagonalen Flächen weniger hochkoordinierte Plätze an den Inselrändern gibt, die den Ausgangspunkt für dendritisches Wachstum bilden können. Durch MC-Rechnungen konnte gezeigt werden, daß der fraktal-kompakt-Übergang sich auf tetragonalen Flächen bei 250 K bis 390 K vollzieht, auf hexagonalen jedoch erst bei 310 K bis 400 K [HZK01/1].

Ein anderer substratinduzierter Wachstumsmodus ist das Wachstum an Stufenkanten. Das Diffusionspotential, das ein Teilchen spürt, wenn es sich einer aufsteigenden Stufenkante nähert, ist in Abb. A 4 dargestellt. Es existiert hier, wie o. a., ein hoch koordinierter und deshalb besonders bevorzugter Adsorptionsplatz. Die Dekoration der Stufenkanten führt dann zur Erzeugung neuer, genauso hoch koordinierter Plätze (jetzt allerdings aus Adatomen selbst), die wiederum nacheinander bevorzugt besetzt werden. Wird dieser Prozeß immer weiter ausgeführt, "verschieben" sich die Stufenkanten über die gesamte Terrasse, und es kommt zum so genannten step-flow growth.

Wenn sich das Adatom einer absteigenden Stufenkante nähert, spürt es eine besonders erhöhte Diffusionsbarriere (vgl. Abb. A 4), deren Ursache in der lokalen Ladungsdichteverteilung in der Umgebung der Stufenkante liegt. (Die Elektronen in den an der Oberfläche auftretenden Zuständen lassen sich als zweidimensionales Elektronengas auffassen, die zugehörigen Wellenfunktionen als ebene Wellen. Diese werden an Defekten, insbesondere Stufenkanten gestreut und es entstehen Potentialbarrieren. Auf Grund der dort abklingenden Wellenfunktion kommt es zur Ladungsverarmung, die einen Beitrag zum Aufbau der Stufenbarriere von bis zu 50 % leistet [MeB97/1].)

Die Barriere kann Adteilchen, welche nicht genügend Energie besitzen, daran hindern, Substratstufen zu überwinden. Diese Barriere wird Ehrlich-Schwoebel-Barriere (oder einfach nur Schwoebelbarriere) genannt, nach Ehrlich und Hudda, denen dieser Effekt erstmals aufgefallen ist [EhH66/1], und nach Schwoebel, der dazu entsprechende Rechnungen durchführte. Die Wirkung der Schwoebelbarriere kann zu einer Verstärkung des Inselwachstums auf bereits bestehenden Inseln führen und damit zur Entstehung von rauhen Filmoberflächen [BaC95/1]. Dazu kommt, daß die Schwoebelbarriere für homoepitaktische Stufen viel größer ist als für heteroepitaktische, wo es sehr oft zum Abbau von Spannungen kommt (z. B. Ag/Pt(111) vs. Ag/Ag(111)) [BBR95/1].

Haben sich Inseln auf der Oberfläche gebildet, kann es trotzdem noch zu Bildungs-, Umlagerungs- und Auflösungsprozessen kommen. Ein dünner (Submonolagen-) Film aus vielen kleinen Inseln kann nämlich seine totale freie Energie reduzieren, indem er sich in wenige große Inseln umwandelt [RME99/1]. Hier können zwei Effekte beobachtet werden. Bei der Ostwald-Reifung fließt Materie von kleineren zu größeren Inseln, die einen geringeren Dampfdruck besitzen (Gibbs-Thomson-Effekt) [Zin99/1]. Demgegenüber steht der Vorgang der dynamischen Verschmelzung, bei dem ganze Inseln über die Oberfläche wandern und koaleszieren, die Smoluchowski-Reifung. In beiden Fällen entstehen aus vielen kleinen Inseln wenige große, was wie o. a. den thermodynamisch günstigeren Zustand darstellt.

Ein interessantes Beispiel, bei dem mehrere Inselbildungs- und Inselformen zu beobachten sind, ist das System Ag/Pt(111) [Rod96/1, BRR94/1, Bru98/1, RBK94/1]: Zwischen 80 K und 110 K bilden sich auf der Terrasse kleine zufällig orientierte Dendriten, bei etwa 110 K bis 170 K werden dagegen eher symmetrische Fraktale gebildet und die Stufenkanten dekoriert. Bis 300 K wandeln sich diese Inseln in kompakte um, die bei weiterer Temperaturerhöhung an Größe gewinnen.

 

A2.3 - Mono- und Supermonolagen

 

2.3. Mono- und Supermonolagen

Oftmals kommt es bereits vor der Auffüllung der Monolage (zumindest bei Raumtemperatur) zur Bevölkerung der zweiten Adlage. Dabei ist das Wachstum auf dendritischen Strukturen nicht oder schlecht möglich, z. B. Au/Ru(0001), jedoch bevorzugt auf kompakten Formationen, z. B. Cu/Ru(0001) [GGK93/1].

Letztlich ist das Wachstum von Inseln innerhalb einer Lage natürlich begrenzt. Spätestens wenn die entsprechende Lage gesättigt ist, d. h. keine Adsorptionsplätze mehr zur Verfügung stehen, wird die nächste Lage bevölkert. Dies kann zur Folge haben, daß die erste Lage abgeschlossen wird oder daß dreidimensionale Inseln (ohne Abschluß der ersten Lage) entstehen.

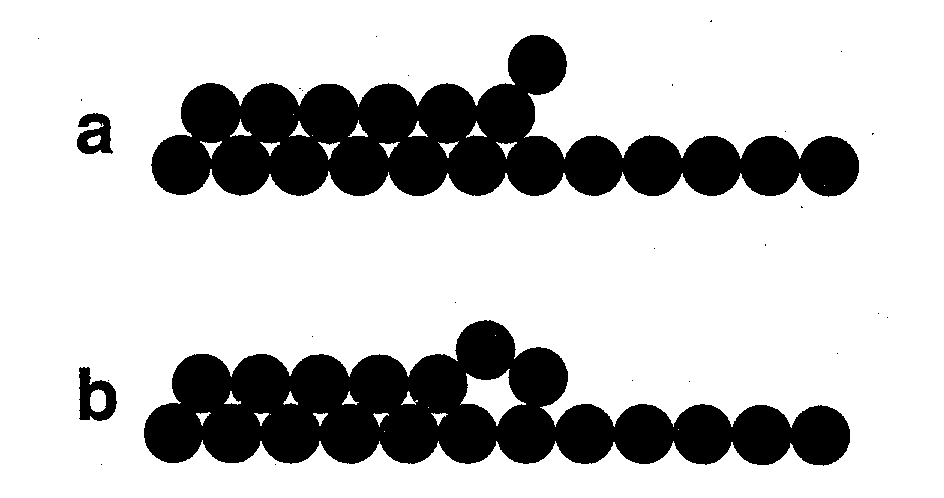
Abbildung A5  Mechanismen für die Kantendiffusions nach [ZLN00/1]: a) bridge-hopping, b) exchange.

Sobald es zur Ausbildung von 3D-Inseln kommt oder man den Fall des Wachstums an oder über Stufen hinweg betrachtet, muß die Stufendiffusion als wachstumsbeeinflussender Faktor mit einbezogen werden. Wie o. a. besteht an Kanten (Substratstufen oder Adsorbatinselränder) eine Diffusionsbarriere. Ein Adteilchen, das diese Barriere überwinden will, muß die dafür nötige Diffusionsenergie besitzen. Ist dies der Fall, spricht man vom Prozeß des bridge hopping. Dieser Sachverhalt tritt zumeist bei glatten Oberflächen bzw. dichten Lagen, wie z. B. fcc(111) sowie eher bei Heteroepitaxie auf. Vorwiegend bei homoepitaktischen Systemen (wo ja die Schwoebelbarriere besonders groß ist, s. o.) und weniger dichten (fcc(100)) bzw. offenen Lagen (fcc(110)), können auch Teilchen, deren Diffusionsenergie nicht ausreichen würde, diese Barriere zu überwinden, trotzdem über die Stufe diffundieren. Bei diesem exchange-Prozeß wechselt das diffundierende Teilchen auf den Adsorptionsplatz des Kantenatoms, welches wiederum einen Platz "weiterrutscht" [ZLN00/1, LLS01/1], vgl. Abb. 5.

Soweit man den Fall der Homoepitaxie betrachtet, können die damit verbundenen Wachstumsprozesse in vier Gruppen eingeteilt werden [Hen96/1]:

• nur Stufenpropagation, keine Keimbildung auf der Terrasse,
• ideales Lagenwachstum mit Keimbildung und Stufendiffusion,
• nicht komplettes Lagenwachstum mit Keimbildung vor Lagenabschluß,
• zufälliges Wachstum ohne Stufendiffusion.

Beim heteroepitaktischem Wachstum fallen weitere Effekte ins Gewicht. Diese höhere Vielfalt rührt daher, daß hier unterschiedliche Stoffe mit verschiedenen strukturellen und elektronischen Eigenschaften miteinander wechselwirken.

 

A2.3.1 - Der "misfit"

 

2.3.1. Der "misfit"

Ein Faktor, der einen entscheidenden Einfluß auf das heteroepitaktische Wachstum nimmt, ist das Mißverhältnis von Adsorbat- und Substratgitter, der misfit. Er wird i. A. wie folgt angegeben:

f =  ( a 0 (substr.) −  a 0 (film) ) / a (substr.) 0

(A1)

Systeme, bei denen die Adatome einen kleineren Atomabstand aufweisen als die Substratatome, haben folglich einen negativen misfit, während der misfit bei größeren Adatomabständen positiv ist. Auf Grund des misfit ist es nicht möglich, daß ein heteroepitaktischer Film völlig spannungsfrei und ohne weitere Effekte auf einem Substrat aufwächst. Während kleine Inseln Verspannungen noch durch Kantenaufweitung abbauen können [BBR95/1], gelingt dies bei größeren Inseln oder gar Lagen nicht mehr. Die Folge können verspannte Filme oder Spannungsabbaureaktionen sein.

Durch den misfit können Adlagen-Morphologien und -Eigenschaften beeinflußt werden. Beim System Dy/Lu(0001) kommt es durch Magnetisierung zu einem Übergang von einer hexagonalen zu einer orthorhombischen Schicht [Fle01/1, ERS87/1]. Auch beim System Ag/Cu(001) wächst das Adsorbat nicht in der vom Substrat vorgegebenen Orientierung auf, sondern, wegen besserer Verwachsungsmöglichkeiten, als (111)-Lage [BCT01/1].

 

A2.3.2 - Der ps-cp-Übergang

 

2.3.2. Der ps-cp-Übergang

Unter pseudomorphem (ps) Wachstum versteht man, daß das Adsorbat mit den vom Substrat vorgegebenen Gitterparametern (hinsichtlich Orientierung und Atomabständen) auf dem Substrat aufwächst. Dies weist auf starke Substrat-Adsorbat-Wechselwirkungen hin und ist natürlich, je nach misfit, mit mehr oder weniger großen Spannungen im System verbunden. Wächst das Adsorbat jedoch mit seinen eigenen Gitterparametern auf dem Substrat auf, kommt es zur Ausbildung einer dichtest gepackten (close packed, cp) Lage, was ein Zeichen für starke Adsorbat-Adsorbat-Wechselwirkungen ist und ebenfalls zu Spannungen im System führt [SLB96/1].

Zwar ist der Übergang zwischen diesen Wachstumsformen oft fließend, doch kann man nach van der Merwe [FrM49/1] anhand des misfit grob entscheiden, welcher Modus für ein bestimmtes System wahrscheinlich ist. Bis zum "kritischen misfit" von 9% sollte ps-Wachstum auftreten und ab dem "Grenz-misfit" von 14% cp-Wachstum. Im Bereich dazwischen lassen sich keine verläßlichen Aussagen treffen. (Eine interessante Parallele läßt sich zu den in Kap. 1.8 angeführten Betrachtungen zur Mischbarkeit zweikomponentiger Systeme gezogen werden: Dort wurde ausgeführt, daß für f < 8%unbergrenzte Mischbarkeit besteht, für f > 15% jedoch Unmischbarkeit.)

Aber auch während des Wachstums, d. h. mit zunehmendem Bedeckungsgrad Q (Verhältnis aus der Zahl der Adatome (der "Monolage") und der Zahl der zur Verfügung stehenden Adsorptionsplätze auf der Substratoberfläche, in [ML]), kommt es dazu, daß beide Wachstumsformen vorliegen können bzw. nacheinander auftreten.

Bei Systemen mit negativem misfit kommt es häufig vor, daß wegen eines starken Substrateinflusses zunächst ps-Wachstum auftritt. Dieser Vorgang dauert bei reinem Lagenwachstum gewöhnlich so lange an, bis genau so viele Adsorbat- wie Substratatome vorhanden sind. Danach werden weitere Atome in die Lage eingebaut, bis sich eine cp-Lage bildet. Beispiele hierfür sind Ni/Ru(0001) [MSB95/1], Cu/Ru(0001) [GSG91/1], Cu/Re(0001) [WSC99/1], Ni; Co; Mo/W(110) [MBT94/1], Pb/W(110) [Bau82/1]. Auch theoretisch konnte das für die fcc(100)-Fläche bestätigt werden [PSZ99/1].

Anders ist der Fall bei Systemen mit positivem misfit, wie etwa Ag/Pt(111) [Rod96/1], Ag/Re(0001) [Sch98/d, PSC97/1, SPC98/1]. Hier kommt es zum Aufbau eines verspannten ps-Filmes schon innerhalb von Adsorbatinseln. Dieser wird als ps-Lage abgeschlossen, und die zweite Lage beginnt zu wachsen. Bereits jetzt ist es nicht mehr möglich, die Verspannungen der nun vorhandenen zwei (zumindest teilweise aufgebauten) Lagen aufrechtzuerhalten, und es kommt zur Relaxation, bei der dann auch Atome aus der ersten Lage empor gehoben werden. Es bildet sich schließlich ein zweilagiger cp-Film aus. Beim System Cu/Pd(100), bei dem für Bedeckungsgrade von < 1 ML ps- und > 3 ML cp-Filme existieren, kommt es im Bereich dazwischen zu einem temperaturabhängigen ps-cp-Übergang: für T < 370 K hat der Film ps-, darüber cp-Struktur [HKW95/1].

Allgemein kann man sagen, daß ps-Filme oft nur in der ersten Lage stabil sind, da die Verspannungen der sich aufbauenden mehrlagigen Schicht zu groß werden, siehe auch Kap. 2.4. Ausführlich befassen sich van der Merve und Bauer in zwei umfangreichen Artikeln mit diesem Thema anhand des Systems Ni/Mo(110), welches nach anfänglicher (1x1)-LEED-Struktur in eine (8x2)-Phase übergeht [MBT94/1, MBT94/2].

 

A2.3.3 - Spannungsabbau

 

2.3.3. Spannungsabbau

Wie bereits festgestellt, kommt es beim Auftreten von Spannungen in heteroepitaktischen Filmen zu Prozessen, die versuchen, diese Verspannung rückgängig zu machen. Derartige Vorgänge sind die Bildung von Moiré-Strukturen, Dislokationen, Rekonstruktionen, Rotationen und/oder Legierungen [Kur99/d, GBD01/1].

Wellungen der Oberfläche, die auf eine inkommensurate (z. B. cp-) Adlage zurückzuführen sind, stellen das am häufigsten beobachtetes Phänomen dar, das zum zweidimensionalem Spannungsabbau führt. Es kommt dabei zur ein- oder auch zweidimensionalen bzw. uni- oder biaxialen (Re-) Expansion/Kompression des Adsorbates, das mit seiner eigenen Gitterkonstante z. B. unter Bildung von Doppelsträngen oder auch in zwei Dimensionen (Bildung von Moiré- Strukturen) auf dem Substrat aufwächst.

Das führt dann dazu, daß Adatome auf besonders günstigen, hochkoordinierten, also energetisch wie auch strukturell tief liegenden Positionen gebunden sind (z. B. Muldenplätze) und andere auf höher liegenden Positionen (z. B. on top). Die Größe der sich daraus ergebenen Einheitszelle richtet sich nach dem Verhältnis der Gitterparameter von Adsorbat und Substrat und ist um so größer, je kleiner dieses Verhältnis ist. Meistens kommt es zu einer Wellung der Adlage (z. B. Co/Pt(111)), aber auch die Substratoberfläche kann unter dem Einfluß einer glatten Adlage, insbesondere bei positivem misfit, gewellt sein (z. B. Pt/Co(0001)) [GBD01/1]. Dies konnte auch durch Rechnungen bestätigt werden [TGL96/1]. Beim System Ag/Cu(111) wird durch die (9 x 9)-Moiré-Struktur der ersten Lage die Absenkung der on top-besetzten Cu-Atome induziert, wodurch die Wellung der Adlage verringert werden kann [Foi93/1]. Tritt unter den oben beschriebenen Voraussetzungen gar keine Wellung auf, so kommt es auf jeden Fall zu einer stärkeren Überlappung der Orbitale von Adsorbat und Substrat, mit der Konsequenz, daß eine besonders starke Bindung zwischen Adatom und Unterlage eintritt.

Dislokationen (dl) sind Liniendefekte, die orthogonal zu den Vorzugsrichtungen des Kristalls sind. Durch diese werden Bereiche voneinander abgeteilt, in denen die Adteilchen mit relativ wenig Verspannungen annähernd pseudomorph auf der Substratoberfläche sitzen. Der misfit wird hierbei wie bei kleinen Inseln (s. o.) durch Relaxation der Kanten ausgeglichen. Bei den Systemen Au/Ni(111) [Bru98/1, JPB95/1] und Cu/Pt(111) [HNW97/1, HNW98/1] treten im STM-Bild bei einer Bedeckung von 0,25 ML Au dreieckige Dislokationsstrukturen mit einer Kantenlänge von drei bis vier Atomen auf. Auch beim System Co/Re(0001) [Par96/d] kommt es auf Grund von Legierungsbildung zu dreieckigen Dislokationsstrukturen.

Bei einer Vielzahl von bimetallischen Systemen induziert die Deposition des Admetalls eine Rekonstruktion der Substratoberfläche. Besonders hervorzuheben ist in diesem Zusammenhang der Prozeß der Facettierung, bei dem sich z. B. eine glatte Oberfläche in eine rauhe umwandelt. Die dabei entstandenen Facetten sind gewöhnlich entlang der Vorzugsrichtungen des Substrates orientiert. Bekannt für ihre Facettierungsneigung sind die (111)-Oberflächen von Wolfram und Molybdän [Rod96/1]. So kommt es beim System Pt/W(111) bei Monolagenbedeckungen und Temperaturen ab etwa 800 K zur Ausbildung von pyramidalen (211)-Facetten [MSD91/1, MGD93/1, DSS93/1, PHK99/1, NiM97/1].

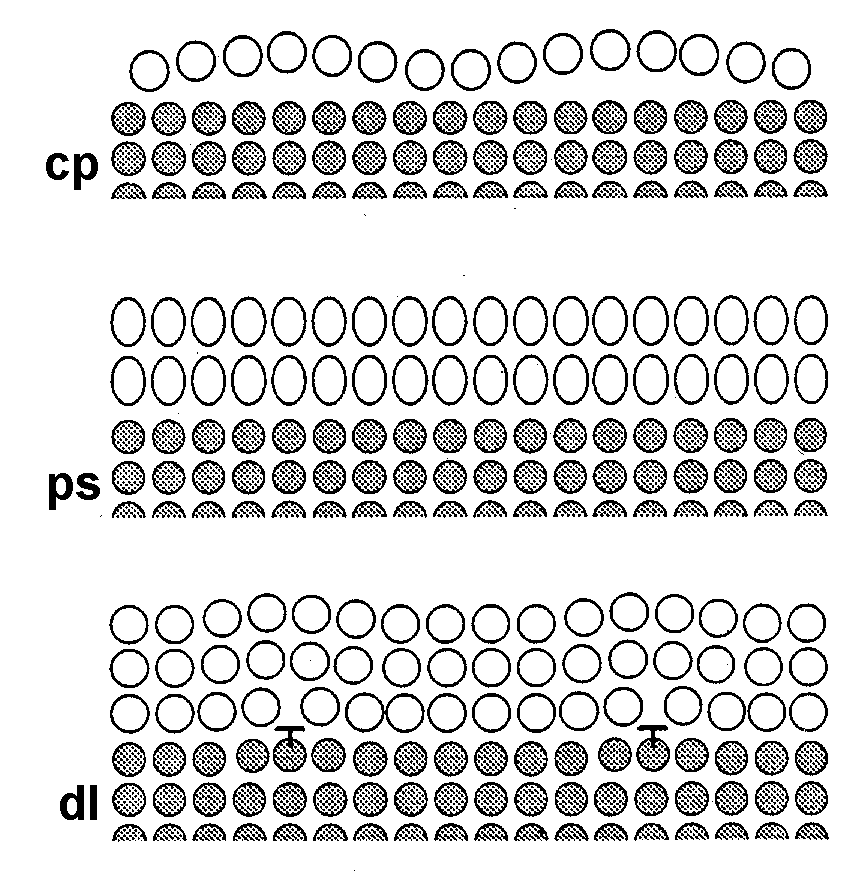
Abbildung A6  heteroepitaktische Wachstumsformen nach [Hen96/1]: cp floating mode, ps pseudomorphic mode, dl dislocation mode.

Systematische Untersuchungen von Rodriguez an den Systemen Pt; Pd; Au; Rh/W(111) und Pt; Pd; Au/Mo(111) stellen den Zusammenhang zwischen Elementeigenschaften und der Fähigkeit des Adsorbats zur Facettierungsinduzierung heraus [Rod96/1, GCM95/1]. Offenbar ist die Triebkraft zur Facettierung die Absenkung der freien Oberflächenenergie. Infolgedessen neigen Adsorbate mit hoher Oberflächenenergie, wie Pd oder Au im Gegensatz zu Adsorbaten mit geringer Oberflächenenergie, wie Cu oder Ag, zur Facettierung. Ebenso scheinen Adsorbate, deren Pauling-Elektronegativität größer als 2 ist, zur Induzierung der Facettierung zu neigen [GCM95/1].

Insgesamt läßt sich das Wachstum in der Mono- und Supermonolage für metallische heteroepitaktische Systeme in drei Klassen einteilen, wie Henzler gezeigt hat [Hen96/1], siehe Abb. 6:

• floating mode (cp): Ausbildung von inkommensurablen Adlagen
• pseudomorphic mode (ps): Wachstum von pseudomorphen, aber gestreckten bzw. gestauchten Filmen
• dislocation mode (dl): Entstehung von Dislokationen in pseudomorphen Filmen zum Spannungsabbau

 

A2.4 - 3D-Wachstum

 

2.4. 3D-Wachstum

Zur weiteren Klassifizierung der Wachstumsvorgänge bimetallischer epitaktischer Systeme bis in dicke Adsorbatschichten dient allgemein eine Einteilung in drei Wachstumsmodi, die von Bauer vorgeschlagen wurden [Bau58/1], siehe Abb. A 7.

Demnach unterscheidet man in:

• Inselwachstum (Volmer-Weber-Wachstum, VW),
• Lagenwachstum (Frank-van-der-Merve-Wachstum, FM),
• Lage + Inselwachstum (Stranski-Krastanov-Wachstum, SK).

Zu quantitativen Aussagen kann man allerdings nicht gelangen, da diese Einteilung anhand von rein thermodynamischen Gesichtspunkten vorgenommen wurde und damit wesentliche Parameter, speziell die Oberflächenenergie, als makroskopische Größe im submikroskopischen Bereich andere Werte (z. B. durch interne Wechselwirkungen) annehmen kann. Von Vorteil ist jedoch, daß meistens allgemeingültige qualitative Aussagen getroffen werden können.

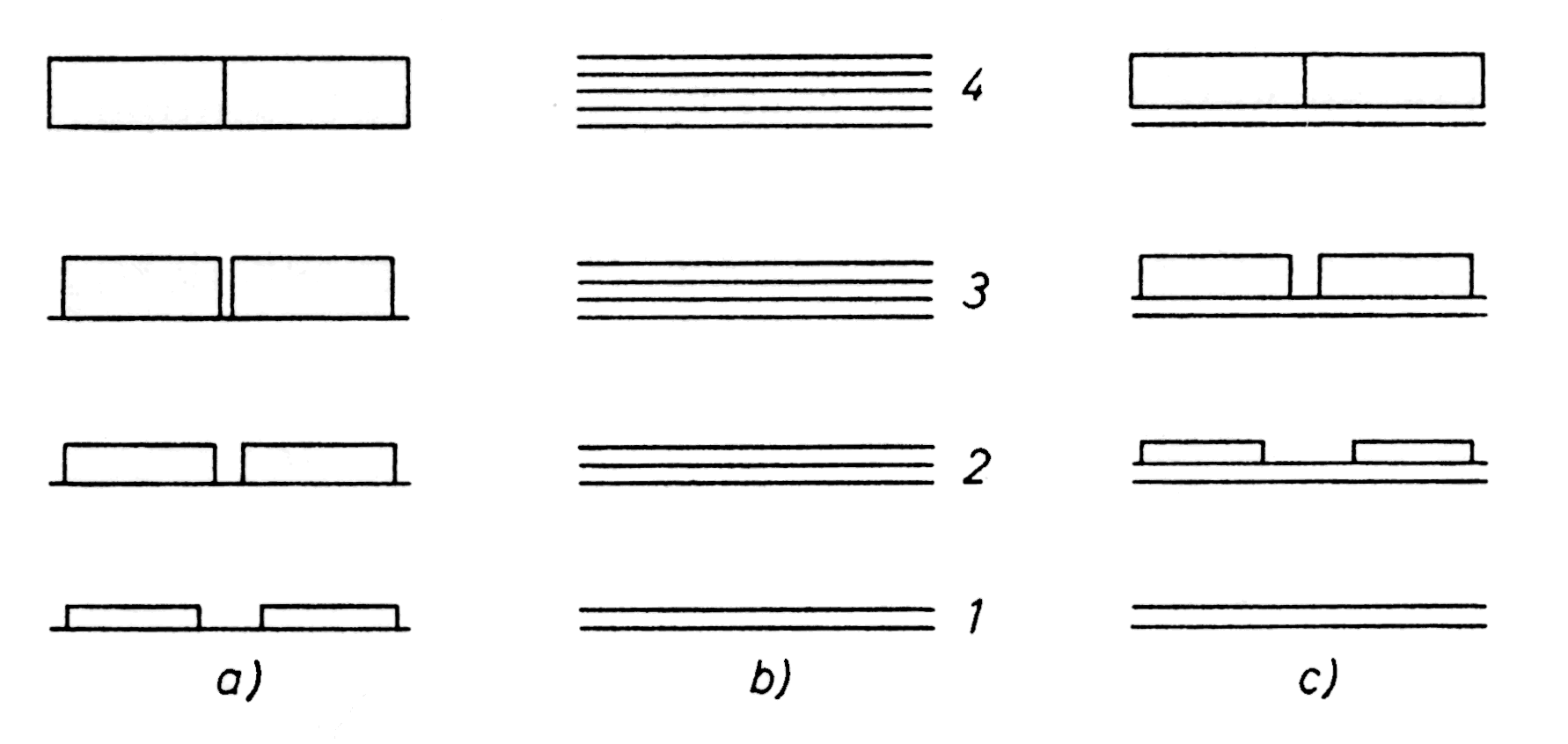
Abbildung A7  Die verschiedenen Wachstumsmechanismen nach Bauer [Bau58/1]: a) VW-Mechanismus, b) FM- Mechanismus, c) SK- Mechanismus.

Aus dem Verhältnis der Oberflächenenergien der beteiligten Komponenten läßt sich nach dem Verfahren von Bauer abschätzen, nach welchem Wachstumsmodus sich ein beliebiges metallisches, epitaktisches System verhält, sofern allerdings keine kinetischen Hemmungen vorliegen. (Oberflächenenergien (freie Überschußenergie pro Fläche) erhält man aus Messungen der Oberflächenspannung der flüssigen Phase und Extrapolation auf T = 0 K [VRS98/1].)

Δσ = − σ S  +  σ A  +  σ I

(A2)

Darin ist s_S die Oberflächenenergie des Substrates (bzw. der obersten Adsorbatlage bei dickeren Filmen), s_A die des aufwachsenden Adsorbates, und s_I ist die interface-Energie. Diese beinhaltet alle im Grenzbereich Substrat/Adsorbat auftretenden chemischen Wechselwirkungen, Spannungen usw.. (Bei negativer Interface-Energie kann es zur Legierungsbildung kommen, bei positiver kann Phasentrennung auftreten [Ter95/1]). Die Größe der interface-Energie ist im Allgemeinen viel geringer als die Oberflächenenergien und fällt erst dann entscheidend ins Gewicht, wenn der Unterschied der Oberflächenenergien gering ist, etwa bei Homoepitaxie oder dem Wachstum auf Adsorbatschichten. Nach Bauer und van der Merve [BaM96/1] ist reines Lagenwachstum zunächst grundsätzlich nur für den Fall der Homoepitaxie zu erwarten, da hier s_S = s_A gilt und der misfit f = 0 ist.

Für den Fall des Wachstums eines zunächst dünnen (< 1 ML dicken) heteroepitaktischen Filmes wird s_A-s_S im Verhältnis zur Interfaceenergie jedoch überwiegen, und es lassen sich zwei Fälle unterscheiden (vgl. Abb. A 7):

1. Ds > 0: Unter dieser Bedingung kommt es unmittelbar zum Aufwachsen dreidimensionaler Keime. Dabei kann das System durch das "Freihalten" von möglichst viel Substratoberfläche mit geringer Oberflächenenergie die Gesamtoberflächenenergie klein halten. Es tritt Inselwachstum (VW) ein.
2. Ds < 0: Bei einer Substratoberfläche, die mit einer übersättigten Adsorbatphase wechselwirkt, deren Atome eine Schicht mit einer wesentlich kleineren Oberflächenenergie bilden, kommt es zur Entstehung einer geschlossenen Lage. Gilt diese Bedingung auch für alle weiteren aufwachsenden Lagen, ist Lagenwachstum (FM) zu erwarten. Dabei steigt nach Bauer [Bau58/1] die Adsorbat-Schichtdicke mit s_A.. Nach Franck und van der Merve ist FM-Wachstum für Systeme zu erwarten, deren misfit f < 9% ist.

Unter Berücksichtigung weiterer Prozesse und bei genauerer Betrachtung des Systems können weitere Wachstumsmodi formuliert werden:

3. Bei höherer Aufdampfrate und geringer Temperatur kommt es zu einer hohen Nukleationsrate und damit zur Bildung von vielen kleinen Inseln. Mit Vergrößerung des Bedeckungsgrades und damit auch der Inseldichte fließen diese zusammen und bilden eine geschlossene Lage. In diesem Fall spricht man vom pseudo-FM-Wachstum.
4. Bei vielen Systemen ist Ds < 0 noch für die erste (oder die ersten wenigen) Adlage(n) gegeben. Beim Aufwachsen einer zweiten Lage (bzw. mit steigender Adlagenzahl) verringert sich Ds jedoch immer mehr, da s_S jetzt zunehmend durch das Adsorbat bestimmt wird. In diesem Stadium fällt besonders die Wirkung von s_I ins Gewicht, welches auf Grund eines großen misfit beispielsweise besonders stark positiv wird [BaM86/1]. Es kommt dann dazu, daß Ds  > 0 wird und auf der (den) ersten Lage(n) 3D-Kristallite aufwachsen. Es tritt also Lage+Inselwachstum (SK) ein.

Nicht nur der (Gitter-) misfit kann als Kriterium für Lagenwachstum herangezogen werden, sondern auch die Fehlanpassung der Oberflächenenergie G_SA [BaM86/1]. Mit G_SA < 0,5 ist demnach die Ausbildung einer geschlossenen Lage möglich, mit G_SA > 0,5 nicht.

Γ SA  = 2⋅|  ( σ S  −  σ A ) / ( σ S  +  σ A )  |

(A3)

Wachsen anfänglich Filme noch pseudomorph auf dem Substrat auf, kommt es mit zunehmender Schichtdicke dazu, daß die Verspannungen innerhalb der Lagen größer als die Wechselwirkungen des Substrates und der ersten Adlage werden. Dies kann auch dazu führen, daß der Film aufreißt. Nach Rechnungen von Levy et al. bilden sich bei einem misfit von -10 % nur zwei Lagen, anschließend findet 3D-Wachstum statt. Bei einem misfit von +10 % hingegen ist das Wachstum für die ersten fünf Lagen zweidimensional [TGL96/1]. Auch Dislokationen in der ersten Lage regen ab einer Dicke des Films, bei dem Pseudomorphie instabil wird, den Übergang vom FM- zum SK-Wachstum an [Mer00/1]. Für viele Systeme ist ein temperaturbedingter Übergang vom pseudo-FM- oder FM-Wachstum (bei Raumtemperatur) zum SK-Wachstum (bei erhöhten Temperaturen) vorherrschend, z. B. Ni/Ru(0001) oder Ni/W(100) [Rod96/1].

5. Bei bestimmten Systemen, bei denen z. B. die Diffusion über Inselränder auf Grund der Schwoebelbarriere inhibiert ist, kann es eigentlich nicht zur Ausbildung von geschlossenen Lagen kommen, s. o.. Trotzdem kann es teilweise gelingen, Lagenwachstum zu erreichen. Man benutzt hier (meistens systemfremde) Substanzen, die ähnlich einem Katalysator wirken. Diese werden Surfactants (surface activating agents) genannt, wenn sie nach dem Wachstum einer Adsorbatlage wieder "obenauf schwimmen" und Interfactants (interface activating agent), wenn sie zwischen Substrat und Adsorbat bleiben. Sie ändern die Oberflächenenergie [Hen96/1] oder ermöglichen, besonders bei erhöhten Temperaturen, den in Bezug auf die Schwoebelbarriere energetisch bevorzugten Austauschdiffusionsprozeß [Fet96/1]. (Dies geschieht z. B. bei Chemisorption eines elektronegativen Materials wie O₂ durch Auswärtsrelaxation der Inselränder [BRR95/1] [BaS01/1]. Die Schwoebelbarriere kann auch mittels Sur(Inter)factants dadurch indirekt verringert werden, daß die Diffusionsbarriere zwischen Terassenplätzen angehoben wird [VVM94/1].

Beispiele für das Wirken von Surfactants sind O₂ in Pt/Pt(111) [BBR95/1], in Cu/Pt(111), Cu; Co/Cu(111) und in Cu/Ru(0001) [KSC93/1, RCT99/1], wo durch DF-Messungen bis zu 80 (!) Lagen [SWW94/1, WSW93/1] und durch STM-Messungen 15 Lagen [WMA97/1, MAW99/1] beobachtet werden konnten. Beim System Au/Ru(0001) bewirkt die Koadsorption von 0,05 ML Schwefel eine Erhöhung der Inseldichte auf das 600-fache [HSB97/1]. Auch Metalle können als Surfactant wirken: Pb in Cu/Cu(111) [CCC99/1], Sb in Ag/Ag(111) [VVM94/1], bzw. in Au/Cu(111) [NoB01/1] As; Sb; Ga; Te in Ge/Si(111) [Hen96/1] oder Au in Ni/Au(001) [AGM01/1], aber auch als Interfactants, z. B. Pb/1 ML Ag/Si(111) [ScB01/1].

 

A2.5 - Oberflächenlegierungen

 

2.5. Oberflächenlegierungen

Wie in Kap. 2.3.3 beschrieben, kann für ein binäres heteroepitaktisches Metallsystem die Bildung einer Oberflächenlegierung Gitterspannungen abbauen helfen. Dies kann sogar zur Folge haben, daß Metalle miteinander legieren, die im dreidimensionalen Zustand nicht mischbar sind (s. Literaturtabelle) bzw. daß Metalle, die eine geordnete Volumenlegierung bilden, an der Oberfläche nur in einer ungeordneten Legierungsphase vorliegen bzw. umgekehrt.

Andererseits kann man eine Oberflächenlegierung auch als zweidimensionalen Abschluß einer Volumenlegierung betrachten [PoR00/1]. Solche Volumenlegierungen können allgemein auf verschiedene Arten terminiert werden. Beispielsweise kann als Zeichen einer hohen Segregationstendenz des einen Legierungspartners dieser in reiner Form an der Oberfläche vorliegen. Es kann sich aber auch eine gemischte (stöchiometrische) Oberfläche auf Grund einer hohen Ordnungstendenz ausbilden. Die Entropie des Systems kann hier als eine Triebkraft angesehen werden, deren Wirkung sich (mit steigender Temperatur) sehr gut am System Cu₃Au(100) beobachten läßt. Ab ca. 400°C kommt es zur Abnahme der Konzentration des Au in der ersten und einer Zunahme in der zweiten Lage unter Ausbildung von nicht stöchiometrischen Anordnungen [SBM91/1].

Oberflächenlegierungen können wegen der hohen Zeitkonstante für die Diffusion ins Volumen allgemein als metastabil angesehen werden [CRS97/1]. An der Grenzfläche einer Volumenlegierung wird die verringerte Symmetrie der Oberfläche wirksam, und es können sich reversible Phasenübergänge vollziehen, die im Volumen so nur bedingt ablaufen können.

 

A2.5.1 - Oberflächenenergien

 

2.5.1. Oberflächenenergien

Die Frage, ob ein epitaktisches Metall-auf-Metall-System, das im Volumen legieren kann, tatsächlich eine Oberflächenlegierung ausbildet, oder ob es zur Entstehung von Adsorbatinseln kommt, kann grob durch einen Vergleich der "Adsorbat-" und "Substratenergien" beantwortet werden [ESJ94/1].

Dabei wird als Substrat- (bzw. Adsorbat-) Energie der auf das Volumen normierte energetische Beitrag einer (einatomigen) Verunreinigung der ersten Substratlage (bzw. pseudomorphen Adsorbatlage) bezeichnet. Demnach ist die Legierungsbildung energetisch begünstigt, wenn die Adsorbatenergie größer ist als die Substratenergie.

Nørskov und Besenbacher [CRS97/1] können in weiterführenden Betrachtungen aus dem Verlauf der Oberflächen-, Segregations- und Mischungsenergie (sowie der Mischungsentropie) mittels DFT-Berechnungen konkrete Voraussagen über das Legierungsverhalten verschiedener 2D-Legierungssysteme machen. Als Oberflächenenergie der Legierung e Leg OF wird der Oberflächenanteil der Gesamtenergie des Legierungssystems (pro Oberflächenatom) bezeichnet. Daraus ergeben sich die Mischungsenergie e mix OF   und die Segregationsenergie e segr OF (als Ableitung der Mischungsenergie nach dem Molenbruch X):

e mix OF  =  e Leg,1ML OF − e 0ML OF −X⋅( e Sep,1ML OF − e 0ML OF )

(A4)

e segr OF  =  d  e Leg,1ML OF d X

(A5)

(mit e 0ML OF  ... Oberflächenenergie des reinen Substrates; e Leg,1ML OF  ... Oberflächenenergie bei vollständigen Mischung und e Sep,1ML OF  ... Oberflächenenergie bei Separation des Systems, beide mit 1 ML Adsorbat).

Aufgrund des Verlaufs der Oberflächenenergie lassen sich pseudomorphe Legierungssysteme in vier Klassen einteilen. Ist die Segregationsenergie des Adsorbates negativ (Abb. A 8, obere Reihe), bleibt dieses in der Adlage. Im Falle einer positiven Segregationsenergie kommt es eventuell zu einer Lösung des Adsorbats im Volumen. Die Oberflächenenergiekurve ist durch eine weitere Eigenschaft gekennzeichnet, die Krümmung. In ihr spiegeln sich zusätzliche Wechselwirkungen innerhalb der Oberflächenlage wider, die beispielsweise durch den misfit ausgelöst werden können. (Bei einer idealen Mischung, in der alle Atomanordnungen energetisch gleichwertig sind, oder auch bei der Bildung von großen Inseln aus reinen Stoffen können diese zusätzlichen Wechselwirkungen minimiert bzw. ausgeschaltet werden, um die Gesamtenergie des Systems zu erniedrigen.)

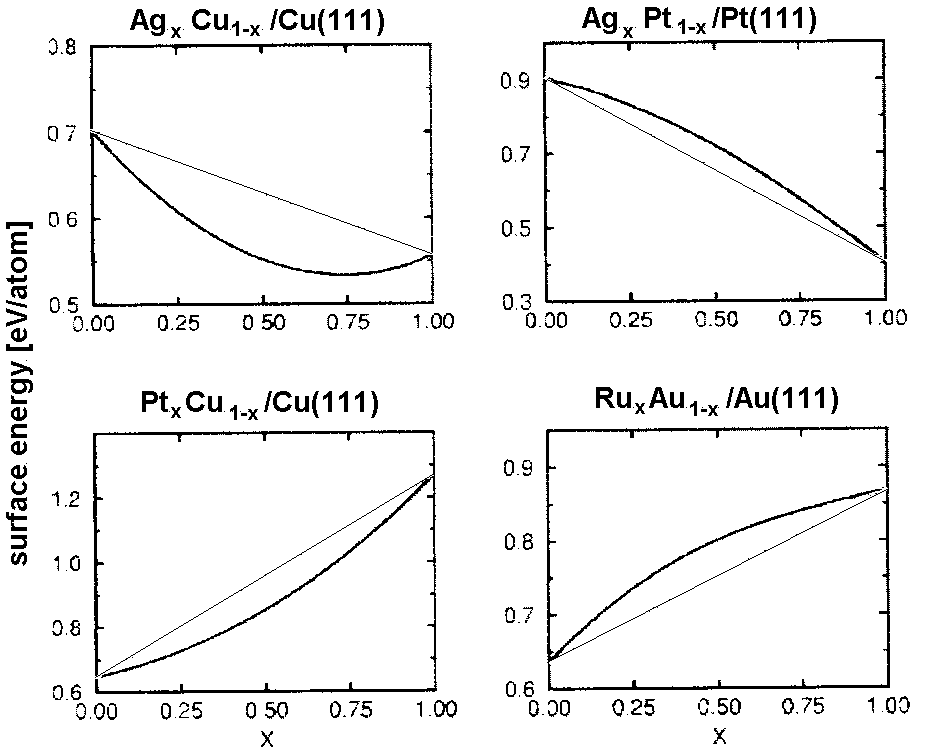
Abbildung A8  Abhängigkeit der Oberflächenenergie- Kurven von der Mix- und Segretationsenergie nach [CRS97/1]; die dünnen Linien entsprechen dem Grenzwert einer idealen Lösung ohne Überschußinteraktionen.

Die geraden Verläufe in den binären Zustandsdiagrammen von Abb. A 8 stellen also die Grenzen zwischen Mischbarkeit und Phasenseparation dar. Ein Verlauf oberhalb der Geraden kennzeichnet eine negative Mischungsenergie und damit die Möglichkeit zur Inselbildung. Zur Legierungsbildung kann es bei positiver Mischungsenergie kommen, die dann vorliegt, wenn die Oberflächenenergiekurve unterhalb der Geraden liegt.

Durch Kenntnis des Verlaufes von e_S (der Segregationsenergie und der Kurvatur) sollte also jedes System im Hinblick auf seine Mischbarkeit eingeschätzt werden können. Nicht berücksichtigt wurde in diesem einfachen Modell die Bildung geordneter oder cp-Phasen.

Bei kleinen Unterschieden in der Oberflächenmischungsenergie fällt (mit steigender Temperatur) der Einfluß der Mischungsentropie ins Gewicht,

s mix OF  = − k B ⋅[ Xln⁡X+( 1−X )ln⁡( 1−X ) ]

(A6)

und es muß der Verlauf der freien Oberflächenmischungsenergie g mix OF betractet werden

g mix OF  =  e mix OF −T⋅ s mix OF

(A7)

Weiterhin werden bei Nørskov und Besenbacher [CRS97/1] Klassen von 2 ML dicken Legierungssystemen mit positiver Segregationsenergie beschrieben, bei denen das Substrat durch das Adsorbat hindurch diffundiert und seinerseits eine neue Adlage bildet, z. B. Fe+Co/Cu(111) [CRS97/1], Rh/Au(100) [SLG89/1], Fe/Au(100) [BaM87/1] als im Volumen nicht mischbare Systeme oder Pd/Cu(111) sowie Au/Ag(111) als im Volumen mischbare Systeme, bei denen es zum Phasengleichgewicht zwischen Mischungs- und reiner Phase kommen kann.

In den nachfolgenden Tabellen sind einige diese Arbeit sowie wichtige Literatursysteme betreffende Daten aus [CRS97/1] (in eV) aufgeführt. Bei Systemen mit positiver Segregationsenergie de_S/dQ sollte es zum Eindringen des Adsorbates ins Substrat kommen können. Systeme mit positiver Krümmung d²e_S/dQ ² sollten Mischungen bilden können. (Die Daten beziehen sich auf die jeweils dicht gepackten Lagen hcp(0001), fcc(111) und bcc(110).)

	Cu/Re	Ag/Re	Au/Re	Pd/Re	Au/Ag	Ag/Au	Cu/Ag	Ag/Cu
deS/dQ	-1,30	-1,61	-1,21	-0.96	+0,07	-0,04	+0,15	-0,28
d²eS/dQ²	-2,15	-2,01	-0,73	-1,12	+0,27	+0,22	+0,33	+1,00
sAds-sSub	-1,8	-2,4	-2,1	-1,6	+0,3	-0,3	+0,6	-0,6
	Cu/Ru	Ag/Ru	Au/Ru	Pd/Ru	Co/Re	Ni/Re	Pt/Re	Au/Ni
deS/dQ	-1,35	-1,74	-1,52	-1,01	-0,63	-0,87	-0,61	-0,46
d²eS/dQ²	-0,40	-1,11	+0,10	-0,35	-0,54	-1,09	+0,21	+2,86

 

A2.5.2 - Legierungen mit und auf der Oberfläche

 

2.5.2. Legierungen mit und auf der Oberfläche

Als Oberflächenlegierungen lassen sich Mischungen von Metallen bezeichnen, deren Ausdehnung i. A. auf zwei Dimensionen beschränkt ist. (Wenn überhaupt, spielt die dritte Dimension, die Senkrechte zur Oberfläche, nur eine untergeordnete Rolle.) Demzufolge gibt es mehrere Arten solcher Legierungen:

1. Durch Segregation an die Oberfläche kann die Zusammensetzung von Volumenlegierungen im Oberflächenbereich geändert sein. Beispiele für segregierende Volumenlegierungen sind PdX mit X = Cu, Ni, Co, Fe [Rod96/2].
2. Durch Reaktion bzw. Vermischung einer Adsorbatkomponente mit dem Substrat kann es zu einer Legierungsbildung kommen. Ein ausführlich erforschtes Beispiel für eine solche Legierung ist das im Volumen nicht mischbare System Au/Ni, das in unterschiedlichsten Konfigurationen untersucht wurde: Au/Ni(110) [Bru98/1, NBS93/1, PBS93/1], Au/Ni(111) [Bru98/1, JBS95/1], Ni/Au(001) [AGM01/1]. Außerdem sind hier die Systeme Ag/Cu(001) [SLB96/1], Cu/Pt(100) [OSM95/1, RWO96/1] und Co/Cu(111) mit 350 K< T <650 K [ZYF96/1] (als System mit thermisch aktivierter Legierungsbildung, die nur bei genügend großer Diffusionsrate und unterhalb der Zersetzungstemperatur auftritt) zu nennen.
3. Eine weitere Art von Oberflächenlegierungen sind Systeme, bei denen zwei Legierungspartner auf einer inerten Oberfläche vermischt sind. Hier sollte sich der immer irgendwie vorhandene Einfluß des Substrats allein auf die Bereitstellung von periodischen Adsorptionsplätzen beschränken. Nach [AGM01/1] kommt es zur Ausbildung von pseudomorphen Lagen (vgl. Kap. 2.3.2) aus Au_1-xNi_x mit 0,1 < x < 0,6 für die Systeme Au+Ni/X(001) mit X = Au, Pd, Pt. Ebenso wie Au und Ni sind auch Cu und Ag im Volumen nicht mischbar. Trotzdem kommt es auch hier zur Ausbildung einer 2D-Legierungsphase auf der Ru(0001)-Oberfläche, wie von Hwang et al. mittels STM [StH95/1] und Wandelt et al. durch spektroskopische Methoden [SCR94/1, SRH94/1, SSK93/2] gezeigt werden konnte, vgl. auch Literaturtabelle.

 

A2.6 - Elektronische Wechselwirkungen

 

2.6. Elektronische Wechselwirkungen

Metalle sind Elemente, die durch eine starke Delokalisierung der Valenzelektronen charakterisiert sind. Durch die Ausbildung der metallischen Adatom-Substratbindung und evtl. einer Adatom-Adatombindung kommt es zu einer Veränderung der elektronischen Eigenschaften des Systems, besonders aber des Adatoms und auch der Grenzfläche. Allein schon der Abschluß des Metallkristalls wirkt sich ja entscheidend auf die elektronischen Zustände aus.

 

A2.6.1 - Die Adatombindung

 

2.6.1. Die Adatombindung

Es stellt sich die Frage, welche Art von Bindung speziell ein Metalladatom zum Substrat und zu seinen Adatomnachbarn ausbildet. Denkbar wären unterschiedlichste Arten von Bindungen. Immer bestehen sicherlich van-der-Waals-Attraktionen zwischen allen beteiligten Teilchen, doch diese sind sehr schwach im Vergleich zu "chemischen" Bindungen.

In den meisten Fällen wird es auch in Metall-Adsorbatsystemen zur Ausbildung einer Metallbindung mit (vollständiger) Delokalisation der Bindungselektronen über den gesamten Metallverband kommen. Im Falle der Homoepitaxie sollte dies (dadurch, daß optimale Adsorptionsplätze besetzt werden) die Regel sein. Bei heteroepitaktischen Metallsystemen könnte diese Bindungsart durch die Besetzung ungünstiger Adsorptionsplätze gestört sein.

Dabei kann es aber auch zum Ladungstransfer zwischen Adsorbat und Substrat kommen. Dieser ist um so größer, je unterschiedlicher die Elektronendichte der beiden Partner ist. Zusätzlich könnten sich formal kovalente, lokalisierte Bindungsanteile zwischen dem Adatom und dem nächstgelegenen Substratatom bzw. Nachbarn definiert werden. Diese wirken sich insbesondere auf die lateralen Wechselwirkungen aus und können attraktiv oder repulsiv, kurz- oder langreichweitig sein.

Nach Rodriguez [Rod96/1, RoG92/1] können die elektronischen Wechselwirkungen der Metalle der Gruppen 8 bis 12 in bimetallischen Oberflächen am besten durch metallische Bindungen mit einem kleinen Anteil ionischen Charakters beschrieben werden. Die stärksten Bindungen treten dabei in Systemen auf, in denen ein Metall mit fast gefüllten Valenzbändern mit einem anderen Metall kombiniert wird, dessen Valenzbänder fast leer sind (bzw. umgekehrt) und es so zu einem starken Ladungstransfer kommen kann. Pd, das ein fast volles d-Band besitzt, bildet die stärksten Bindungen zu Substraten aus, die ein fast leeres Valenzband besitzen. Dies zeigt sich in der Lage der Monolagentemperaturen im TDS und in der Verschiebung des 3d5/2-Peaks eines Monolagenspektrums gegenüber Pd(100) im XPS [Rod96/1]:

Pd/Substrat [4d85s2]	Ta(110) [5d36s2]	W(110) [5d46s2]	Re(0001) [5d56s2]	Ru(0001) [4d65s2]	Rh(111) [4d75s2]
TDS [K]	1540	1510	1450	1440	1390
XPS [eV]	+0,9	+0,8	+0,7	+0,3	+0,2

Wie aus der Tabelle zu entnehmen ist, erhält man tatsächlich die höchsten Desorptionstemperaturen für Ta mit einem relativ leeren d-Band. Die XPS-Peakverschiebungen sind alle positiv, was auf einen Ladungstransfer vom Pd zum Substrat deutet, und sind am stärksten für Ta. Cu[3d¹⁰4s¹], dessen 4s-Band halb gefüllt ist, sollte die stärksten Bindungen zu Metallen mit fast vollen oder fast leeren Valenzbändern ausbilden können. Auch dieser Fakt läßt sich durch der Lage der Monolagentemperaturen im TDS und die Verschiebung des 2p_5/2-Peaks eines Monolagenspektrums gegenüber Cu(100) im XPS verifizieren [Rod96/1]:

Cu/Substrat	Ta(110)	W(110)	Re(0001)	Ru(0001)	Rh(111)
TDS [K]	1260	1220	1180	1210	1265
XPS [eV]	+0,28	+0,08	+0.02	-0,12	-0,41

Erwartungsgemäß hat Cu auf Substraten mit vollen oder leeren Valenzbändern die höchsten und auf Re, dessen d-Band halb gefüllt ist, die geringste Desorptionstemperatur. Auf Ta und W wirkt Cu eher als Elektronendonor und auf Ru und Rh eher als Elektronenakzeptor, was am Vorzeichen der Peakverschiebung sichtbar wird und, wie o. a., mit der unterschiedlichen Elektronendichte der Substrate begründbar ist.

Auch die Elektronegativität der Atome an der Oberfläche hat Einfluß auf die Polarität der Adsorbat-Substrat-Bindung. Allerdings kann diese erheblich von der "normalen" Elektronegativität (der Volumenatome) der Metalle abweichen. Solch ein Effekt resultiert aus der veränderten Symmetrie an der Oberfläche und der damit ebenfalls veränderten Beteiligung der verschiedenen Orbitale. Beispielweise hat Pd an der Oberfläche eine größere Elektronegativität als Cu und die Reihenfolge der gängigsten Substrate verändert sich nach: Ta(110) > W(110) > Mo(110) > Re(0001) > Ru(0001) > Rh(100) [RoG92/1].

 

2.6.2 - Elektronische Oberflächeneffekte

 

2.6.2. Elektronische Oberflächeneffekte

Auch ohne Adsorbatschichten liegt auf Metalloberflächen eine Dipolschicht vor. Dies resultiert daraus, daß die Schicht der nächsten Nachbarn für die Oberflächenatome fehlt und damit ihre Wellenfunktion (das Elektronengas des Metalls) ins Vakuum expandiert. Es kommt so zur Ausbildung einer negativen Schicht außerhalb des Kristalls und einer positiven Kompensationsschicht unter der Oberfläche. Eine physikalische Größe, die sensitiv auf solche Oberflächeneffekte reagiert, ist die Elektronen-Austrittsarbeit eF . Diese wird (scheinbar, da es Metalloberflächen ohne Dipolschicht nicht gibt) bei dem oben beschriebenen Prozeß erhöht. Es handelt sich bei eF um die Arbeit, die geleistet werden muß, um ein Elektron aus dem Festkörper ins Vakuum zu transportieren. Sie setzt sich aus zwei Teilen zusammen. Der eine Teil ist das Potential, daß mit dem Überwinden der Dipolschicht verknüpft ist, das Oberflächenpotential c. Der andere Teil ist der Volumenbeitrag der Bindungsenergie der Elektronen im Kristall, also das elektrochemische Potential der Elektronen im Metallverband m (auch Fermienergie E_F) [Smo41/1].

eΦ  = μ−eχ

(A8)

Kommt es zu Veränderungen im Oberflächenbereich des Kristalls, so wirkt sich dies auf c, nicht aber auf m aus. Damit gilt für die Änderung der Austrittsarbeit aus (A8):

ΔΦ =−Δχ

(A9)

Dieser Zusammenhang läßt sich nach Gary und Thomas [GaT56/1] durch Anwendung eines simplen Modells mit der Elektronegativität X_Sub in Verbindung bringen, was eine grobe Abschätzung von eF [in eV] für reine Metalle (Metallsubstrate) zuläßt.

[ eΦ ] = 0,817⋅ X Sub +0,34

(A10)

Der erste Summand wird dabei m zugeordnet, der zweite c. Aus (A9) und (A10) ergibt sich für dicke Adsorbatlagen [in V]:

[ ΔΦ ] = 0,817⋅( X Ads − X Sub )

(A11)

Nicht nur die Begrenzung des Kristalls in der Oberfläche wirkt sich auf die elektronischen Eigenschaften eines Systems aus. Auch die Struktur oder allgemeiner die Morphologie der Oberfläche spielt eine große Rolle.

Auf statistisch oder periodisch rauhen (z. B. gestufte oder grabenförmige) Oberflächen kommt es zu einer Erhöhung der Dichte an Stufenkanten. Je offener eine solche Oberfläche ist, desto stärker ist die Austrittsarbeit erniedrigt. Für Pt tritt beispielsweise an den Stufenkanten eine lokale Erniedrigung der Austrittsarbeit um etwa 1 eV auf [Wan91/1]. Es wird sogar ein linearer Zusammenhang zwischen der Stufendichte und der Abnahme der Austrittsarbeit konstatiert [SCT85/1].

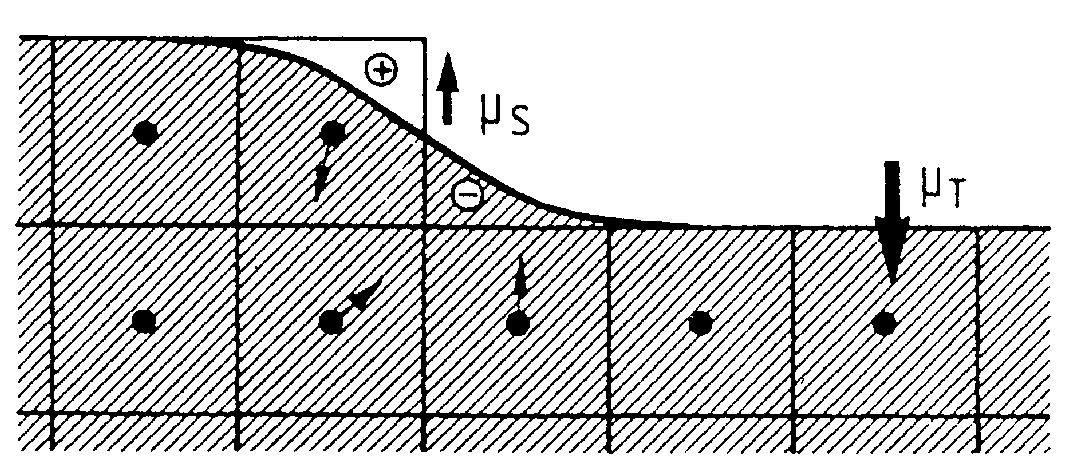
Abbildung A9  Veränderung des Oberflächendipols als Wirkung des Smoluchowski-Effektes nach [Wan91/1].

Diese Ladungsverteilung an Kristallstufen hat ihren Ursprung in der Ausbildung lokalisierter Dipole an den Stufenatomen m_S, die dem normalen Oberflächendipol m_T entgegengesetzt gerichtet sind, vgl. Abb. A 9. Der hier auftretende Smoluchowski-Effekt [LaK70/1] bewirkt, daß die Ladungsverteilung nicht der scharfen Stufengeometrie folgt, sondern daß sich ein "weicher" Übergang vom Stufen- zum angrenzenden Terrassenatom ergibt. Es kommt zu einer Glättung der Elektronenwolke im Metall: "Ladung fließt von den Bergen in die Täler der Oberfläche" [Smo41/1]. Insgesamt wird die Oberfläche dadurch positiviert und so eF verkleinert. Dieser Prozeß läßt sich auf die Oberflächenrauhigkeit verallgemeinern. Je glatter eine Oberfläche ist, desto größer ist eF. (Für die verschieden indizierten, gängigen Metalloberflächen ergeben sich in der Regel Unterschiede von bis zu 0,5 eV. (Gegenüber Cu(111) besitzen z. B. die Cu(100)-Oberfläche eine um -17 meV und die Cu(110) eine um -37 meV veränderte Austrittsarbeit [PoB75/1].)

Die Änderungen, die durch Adsorption von Fremdatomen hervorgerufen werden, sind zumeist entschieden höher. Sie liegen im Bereich einiger 100 meV bis einiger eV. Das Vorzeichen von DF wird dabei von zwei Größen bestimmt. Die eine ist die Richtung des bei der Adsorption auftretenden Ladungstransfers. Wird Ladung ins Substrat verschoben, kommt es zur Verkleinerung von eF. Die andere Größe ist der Unterschied zwischen der Austrittsarbeit des reinen Adsorbats und der des reinen Substrates, wobei insbesondere der Wert der (dünnen) Adsorbatschicht ja wieder vom Ladungstransfer mitbestimmt wird. Nach einem einfachen Kondensator-Modell:

ΔΦ =  Θ⋅ μ Ads / ε 0

(A12)

(mit m_Ads, ... chemisches Potential des Adsorbats und ε₀ ... Dielektrizitätskonstante) besteht für kleine, wenn auch nicht sehr kleine Bedeckungsgrade bei denen m_Ads als konstant angesehen werden kann, ein linearer Zusammenhang zwischen DF und Q.

Für die in dieser Arbeit betrachteten Systeme Cu, Ag, Au/Re ist der Ladungstransfer auf Grund der vergleichbaren Elektronendichten nicht groß, und DF sollte im Wesentlichen vom Unterschied der Elektronen-Austrittsarbeiten der reinen Metalle bestimmt werden. Cu und Ag sollten also nach den Werten aus Kap. 1.6 eF erniedrigen, Au sie erhöhen. Beim System Pd/Re kommt es offenbar zum Ladungstransfer vom Pd zum Re [Rod96/1]. Die Austrittsarbeit ist für beide Elemente etwa gleich (vgl. auch hier Kap. 1.6). In diesem Fall lassen sich keine konkreten Vorhersagen treffen.

		Kapitel A1 - Die verwendeten Proben-Metalle
		Kapitel A3 - Kinetik und Energetik von Oberflächenprozessen