Energetik und Kinetik des Systems Cu/Re(0001) - Diplomarbeit von Ronald Wagner

2. Behandlung von Oberflächenphänomenen

2.1 2D-Wechselwirkungen

2.1.1 Das Teilchen auf der Oberfläche

Befindet sich ein Teilchen auf einer Substratoberfläche, so spürt es die Wirkung eines Multipotentialfeldes, das in einzelne Wechselwirkungskräfte zerlegt werden kann. Die Wechselwirkungen von Adsorbatteilchen können beschrieben werden durch:

• Dipol-Dipol-Wechselwirkungen (die bei niedrigen Bedeckungen zumeist relativ klein sind),
• Überlappung von Atomorbitalen benachbarter adsorbierter Teilchen, besonders bei hohen Bedeckungen,
• Überlappungen von Atomorbitalen mit dem Leitungsband des Substrates,
• indirekte Wechselwirkung der Atomorbitale benachbarter Atome über das Leitungsband.

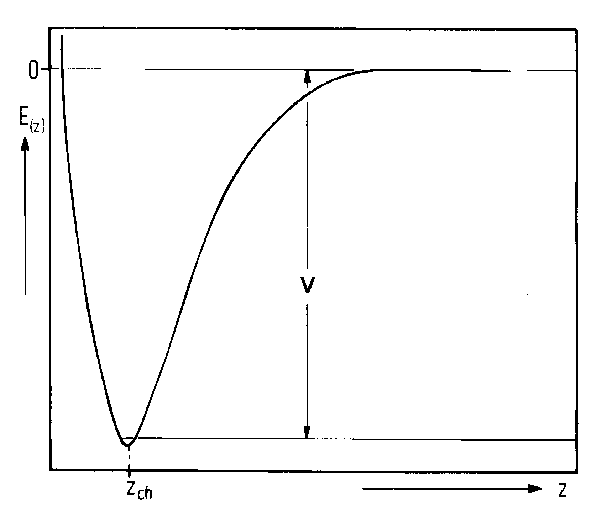
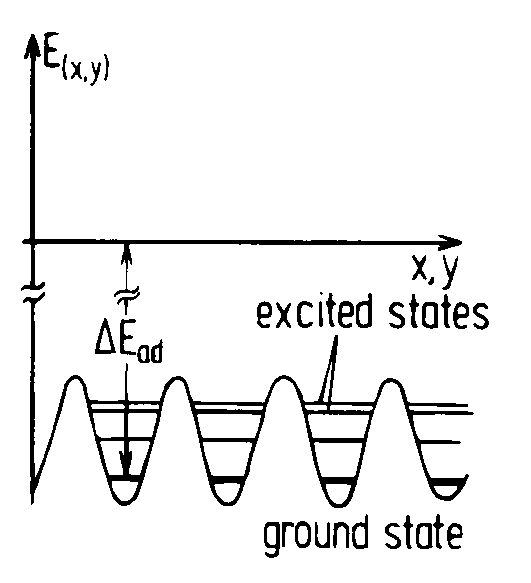
Abbildung 4 Chemisorptionspotential vertikal zur Oberfläche; Abbildung 5 Chemisorptionspotential horizontal zur Oberfläche

Das Teilchen kann an der Oberfläche haften oder es kann desorbieren, wenn seine Energie groß genug ist (k_BT³DE_des) (Abb.4). Weniger Energie benötigt das Teilchen, um sich auf der Oberfläche zu bewegen. Es muß dazu nur die kleineren Potential-barrieren, die sich zwischen den einzelnen Adsorptionsplätze ausbilden, überwinden (E_mig<k_BT< DE_des) (Abb.5).

Als Prozesse auf der Oberfläche, die zu einer Änderung der Bedeckung führen, kommen die Desorption, definiert durch die Desorptionsrate , und die Adsorption, beschrieben durch die Adsorptionsrate , in Betracht, so daß man für die totale Bedeckungsänderung formulieren kann:

(1)

Eine untergeordnete Rolle spielen auch Diffusionsprozesse zum Rand oder zur Rückseite sowie ins Volumen des Substrates.Als einen Ausdruck für die Stabilität eines Zustandes kann man die Lebensdauer des dazugehörigen Teilchens auf der Oberfläche definieren [BAU75]:

t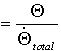 (2)

Bezüglich der Raten können drei Fälle grob unterschieden werden:

• bzw. t : Alle Atome aus der Gasphase adsorbieren oder kondensieren.
• bzw. bzw. : Dies ist der Fall der Gleichge-wichtsbedeckung. (Q₀ ist die Bedeckung vor Beginn des betrachteten Prozesses.)
• : Kein Teilchen aus der Gasphase bleibt an der Oberfläche haften, ausschließliche Desorption.

2.1.2 Theorie des Übergangszustandes (TST) / Theorie der absoluten Rate (ART)

 Den Vorgang der Desorption kann man unter Zuhilfenahme der Theorie des Übergangszustandes (TST) [EYR41] betrachten. Basisidee der TST ist die Annahme, daß der Desorption eine Gleichgewichtsreaktion vorgelagert ist, in der ein ‘aktivierter Komplex’ gebildet wird. Die Desorptionsrate wird durch die Zustandsdichte am Übergangszustand bestimmt, welcher sich am Potentialmaximum oder in seiner Nähe befindet. Vorausgesetzt wird, daß:

• Teilchen, die einmal den Übergangszustand erreicht haben, nicht mehr in den Ausgangszustand zurückkehren,
• die Energieniveaus des Ausgangszustandes thermisch (d.h. nach einer Boltzmann-verteilung) und die des Übergangszustandes statistisch (zufällig) besetzt sind,
• alle Teilchen mit genügender Energie gleich schnell reagieren.

 Für den (desorptions-) ratenbestimmenden Schritt, also das vorgelagerte Gleichgewicht, kann man damit das Massenwirkungsgesetz (MWG) wie folgt formulieren (Z=Zustandssumme, E₀=Nullpunktsenergie) [CHR91]:

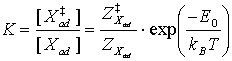(3)

Nach dem Übergang eines Freiheitsgrades der Schwingung des ‘aktivierten Komplexes’ (gegen die Oberfläche) in eines Translationsfreiheitsgrad der Desorption (Separation der Nullpunktsenergie) erhält man für die Gleichgewichtskonstante mit DE_des=Desorp-tionsenergie (Aktivierungsenergie der Desorption am absoluten Nullpunkt):

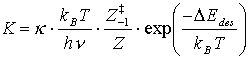(4)

und für die Desorptionsrate:

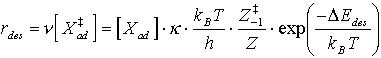(5)

k ist ein Übertragungskoeffizient, der quantenmechanische Effekte (wie z.B. das Tunneln oder die laut Voraussetzung verbotene Rückreaktion (s. o.)) berücksichtigt. Für die hier durchgeführten rein klassischen Betrachtungen wird k=1 gesetzt.

 In Gleichung (5) kann man die (Oberflächen-) Konzentration durch die Bedeckung Q, d.h. die Anzahl der bedeckenden Teilchen pro zur Verfügung stehender Adsorptions-plätze ersetzen. Bezieht man Q auf eine bestimmte Monolage, gilt Q=Q_ML£1. Wird n als präexponentieller Faktor definiert, kann man (5) neu formulieren:

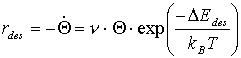(6)

Wendet man (2) auf (6) an, erhält man folgende Beziehung:

t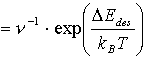 (7)

Aus der Annahme, daß t bedeckungsgradunabhängig ist, leitet Bauer [BAU75] ab, daß n und DE_des zwar nicht auch bedeckungsgradunabhängig sind, daß aber wohl zwischen DE_des und lnn ein linearer Zusammenhang, d.h. ein Kompensationseffekt besteht.

Bezieht man die laterale Wechselwirkung der Adsorbatteilchen mit ein, besteht dieser Effekt nur näherungsweise, da sich die laterale Wechselwirkungsenergie als Summand, nur im exponentiellen Term niederschlägt (vgl. Gleichung (29)).

Betrachtet man n als Geschwindigkeitskonstante im allgemeinen Geschwindigkeits-gesetz einer Reaktion n-ter Ordnung ([X]=Konzentration des Stoffes X),

(8)

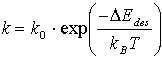und (9)

erhält man so die aus der Thermodynamik wohl bekannte Polanyi-Wigner-Gleichung,

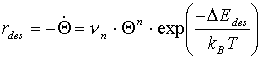(10)

mit n (11)

Bei energetisch unterschiedlichen Adsorptionsplätzen sind mehrere Ratengleichungen nötig. Wenn die Teilchen zwischen Adsorptionsplätzen wechseln können, muß zusätzlich ein Diffusions-term berücksichtigt werden.

Um Aussagen über die tatsächliche Bindungsenergie eines Teilchens machen zu können, ist es nötig, die Desorptionsenergie klar zu definieren. Sie ist die Energie, die einem (Mol) Teilchen zugeführt werden muß, damit es desorbiert, d. h. das chemische Bindungspotential der Oberfläche verläßt. DE_des ist stets positiv.

King [KIN75] konstatiert, daß die Adsorption auf sauberen Metall-Oberflächen generell ein nicht aktivierter Vorgang ist und man die Desorptionsenergie eines Teilchens DE_des mit der Bindungsenergie dieses Adsorbats auf der Oberfläche DH_ads identifizieren kann.

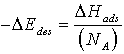(12)

Führt man die Desorptionsentropie ein,

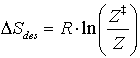(13)

so läßt sich eine exponentielle Abhängigkeit von n und DS_des erkennen:

n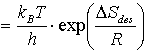 (14)

Dieser Zusammenhang ist auch physikalisch verständlich. Ein Teilchen sollte um so schneller von der Oberfläche desorbieren, je größer der Entropiegewinn dabei ist. Für fest gebundene Teilchen ist demnach der entropische Beitrag zur Triebkraft der Desorption größer als für nur schwach gebundene (vgl. auch 2.1.3 b).

 2.1.3 Das Modell des zweidimesionalen Gases

Adsorptionssysteme mit einer glatten Oberfläche (wie die Re(0001)-Oberfläche) können besonders gut mit Hilfe des Modelles des 2D-Gases beschrieben werden. Dieses Modell basiert auf zwei Komponenten, die sich im Gleichgewicht befinden. Die eine kann sich auf der blanken Substratoberfläche frei bewegen, die andere ist in Adsorbatinseln lokalisiert. Diese kondensierte Phase kann mit dem Einsteinmodell [KRE88] beschrieben werden. (Ein Festkörper soll nach diesem Modell aus einem System gekoppelter Oszillatoren bestehen, deren Schwingungsfrequenz durch n gegeben ist.) Die frei beweglichen Teilchen werden als 2D-Gas angesehen, das ideale Gaseigen-schaften besitzen soll.

Die Desorption ist nach dem o.a. Modell zum einen aus der 2D-Gasphase mit dem Frequenzfaktor n₂ (2D-Gas) oder zum anderen aus der kondensierten Phase mit dem Frequenzfaktor n_c (condensed) möglich.

Die Desorption direkt aus der kondensierten Phase vollzieht sich hauptsächlich im Monolagenbereich. Im Submonolagenbereich gehen Teilchen (nach Kreuzer [KRE88], [PAY88]) zunächst mit n_c2 (cond. - 2D-Gas) in die 2D-Gasphase über und von dort mit n₂ in die 3D-Gasphase.

Dabei können zwei Fälle unterschieden werden:

• n_c2>>n₂: Der Übergang ins 2D-Gas ist so schnell, daß ein Quasigleichgewicht zwischen den beiden Phasen besteht. Das bedeutet, daß alle chemischen Potentiale gleich und alle 2D-Wechselwirkungen null sind. Daraus resultiert eine Desorption nullter Ordnung.
• n_c2<<n₂: Der Übergang ins 2D-Gas ist der langsamste und damit geschwindigkeits-bestimmende Schritt. Die Desorption vollzieht sich hier quasi von den Inselrändern her. Daraus folgt eine gebrochenzahlige Desorptionsordnung. Dies ist z.B. bei Edelgasadsorptionen der Fall [KRE91]. Hier kann nicht von einem Gleichgewichts-zustand ausgegangen werden. Dieser Fall soll hier nicht weiter vertieft werden. (Eine auf diesen Fall bezogene Desorptionsratengleichung ist unter 3.1.4.c zu finden.)

Bauer [BAU75] hingegen nimmt auch für den Submonolagenbereich eine Desorption aus der kondensierten Komponente an, die mit n_2c aus Teilchen der 2D-Gasphase nachgebildet werden. Auch hier ist das System im Gleichgewicht, und eine Desorption nullter Ordnung kann beobachtet werden.

Für die Desorption aus dem Gleichgewicht ergibt sich die Desorptionsrate:

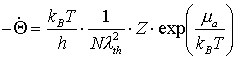(15)

N ist die Gesamtzahl der unterscheidbaren, zur Verfügung stehenden Adsorptionsplätze pro Oberfläche, m_a das chemische Gleichgewichtspotential. l_th ist die thermische Wellenlänge, also ein Maß für die Beweglichkeit der Teilchen.

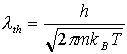(16)

Für das chemische Potential kann man schreiben [KRE91]:

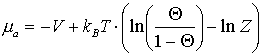(17)

Die gesamte Bedeckungsgradabhängigkeit ist also hier in m_a enthalten. V ist die Potentialtiefe eines Adsorptionsplatzes. Der Faktor 1/(1-Q) berücksichtigt den konfigurellen Entropieeffekt, daß pro Elementarzelle nur ein Adsorptionsplatz zur Verfügung steht. Gollisch [GOL81] ordnet diesen Term dem Einwirken von Precursor-zuständen (Physisorption) zu. Nagai identifiziert diesen Term mit dem Auftreten von ‘aktivierten Zuständen oberhalb besetzter Plätze’ [NAG88]. Er unterscheidet zwischen dem ‘strong correlation limit’, wo jeder Adsorptionsplatz höchstens einfach besetzt werden kann (Q), und dem ‘weak (no) correlation limit’, wo aktivierte Teilchen oberhalb der Adsorbatschicht existieren können, aber nicht physisorbiert sind (Q/(1-Q)) [HIR86].

Betrachtet man die Vorgänge auf der Substratoberfläche, kann die Zustandssumme Z eines Teilchens in mehrere Teile aufgeteilt werden:

(18)

Die molekulare interne Zustandssumme wird Z_int=1 für Atome gesetzt. (Für Moleküle muß berücksichtigt werden, daß Freiheitsgrade bei der Wechselwirkung mit der Oberfläche eingefroren werden können, so daß man für Z_int=Z_int,3D/Z_int,2D setzen muß.)

Z_z ist die Zustandssumme für die Bewegung gegen die Oberfläche und Z_xy für die Bewegung auf der Oberfläche mit:

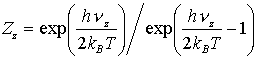(19)

a) Das Teilchen im 2D-Gas

Haben die Teilchen genügend Energie, um sich frei auf der Oberfläche zu bewegen, d.h., befinden sie sich energetisch oberhalb der Potentialbarrieren zwischen den Adsorptionsplätzen, so wird ihre Bewegung nicht oder nur wenig von dem Potential beeinflußt und man kann setzen:

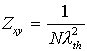(20)

Unter Verwendung der Hochtemperaturnäherung (k_BT>>hn_z) erhält die Desorptions-ratengleichung folgende Gestalt (V=Bindungspotential in z-Richtung):

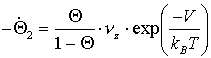(21)

n (22)

b) Das Teilchen in Adsorbatinseln

Für den Fall der vollständigen Lokalisation, d.h. für eine kondensierte Phase muß auch für Z_x und Z_y ein Term wie (19) geschrieben werden und es ergibt sich mit (k_BT>>hn_z):

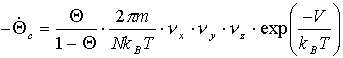(23)

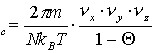n (24)

Typische Werte für die Desorption aus der 2D-Gasphase (mobile Teilchen) sind n₂=10¹²...10¹³s^-1, für die Desorption aus der kondensierten Phase (immobile Teilchen) n_c=10¹⁶...10¹⁷s^-1 [BAU75], [KRE91]. In bezug auf (14) wird hier noch einmal deutlich, daß der Entropiegewinn für die Desorption aus der kondensierten Phase größer ist als der für die Desorption aus der 2D-Gasphase. Beim alleinigen Vorhandensein des 2D-Gases sollte also n=n₂ sein, bei der Desorption aus einer Koexistenzregion oder aus einer rein kondensierten Phase wird n=n_c.

Bauer [BAU75] wendet die Hochtemperaturnäherung (k_BT>>hn_z) nicht an, sondern er setzt:

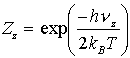(25)

und gelangt zu:

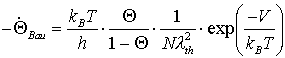(26)

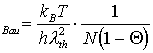n (27)

Weiterhin approximiert er: V=DE_des. Demnach sind in DE_des sämtliche eneretische Wechselwirkungen der Teilchen auf der Oberfläche enthalten.

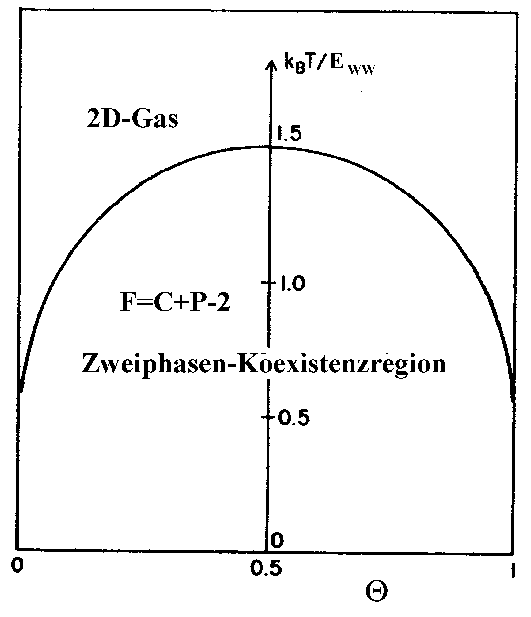
Abbildung 6 Phasendiagramm für das 2D-Gas [NAG86]

Aus dem Phasendiagramm für das 2D-Gas kann man entnehmen, wann das chemische Potential konstant und unabhängig von der Dichte des Systems bleibt, nämlich dann, wenn es im Zweiphasen-Gleichgewicht ist.

Das Zweikomponenten-System hat nach der Gibbsschen Phasenregel F=C-P+2 im Zweiphasengebiet keinen Freiheitsgrad zur Änderung der Bedeckung zur Verfügung, da Druck und Temperatur festgelegt sind [ATK87]. Die Desorption wird dann unabhängig von der Bedeckung, was einer Desorption nullter Ordnung entspricht.

Kreuzer [KRE91] gibt folgende Beziehung für das chemische Potential in der Koexistenzregion an:

(28)

Durch Einsetzen in (15) erhält man die Desorptionsrate:

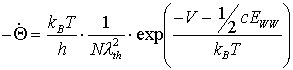(29)

E_WW steht hier für die laterale Wechselwirkungsenergie des betrachteten Adsorbat-teilchens mit seinen nächsten Nachbarn. Diese können attraktiv (negative E_WW) oder repulsiv (positive E_WW) sein. (Für die (0001)-Oberfläche ist die Koordinationszahl c=6, s. Abb.3)

Die Rate für die Desorption aus der Koexistenzregion des 2D-Gases ist deshalb nicht bedeckungsgradabhängig, weil hier der Anstieg der Bedeckung nur zur Veränderung des Verhältnisses 2D-Gas/Kondensat führt.

Nagai postuliert [NAG86], [NAG87], daß eine Desorption nullter Ordnung generell dann beobachtet wird, wenn ein Phasengleichgewicht bei einer Phasenumwandlung erster Ordnung vorliegt.

2.1.4 2D-Morphologie

Günzel [GÜN93] konnte für das System Cu/Ru(0001) im Submonolagenbereich Inselwachstum durch STM-Messungen nachweisen. Ab 0.15ML vergrößerte sich die Anzahl der Inseln nicht mehr, die Größe der Inseln selbst nahm jedoch zu.

Die Kinetik des Inselwachstums kann wie folgt beschrieben werden [GÜN93]. Zunächst kollidieren zwei (frei im 2D-Gas bewegliche) Atome miteinander, bzw. an und mit Kanten oder anderen Oberflächeninhomogenitäten. Bevor der so gebildete Cluster dissoziiert, kollidiert ein weiteres Teilchen usw.. Um nicht zu zerfallen, muß ein solcher Cluster eine minimale Größe haben. Diese Größe wird als kritische Clustergröße (CCS-Critical Clustersize) bezeichnet. Die CCS hängt sowohl von der Wechselwirkungs-energie der Adsorbatteilchen ab als auch von der Dichte des 2D-Gases, der Mobilität der Atome, der Desorptionsrate und der Substrattemperatur. Für Metall-Metall-Systeme kann man CCS=1 annehmen.

Pötschke (PÖT91) fand für das System Cu/Ru(0001) schon bei sehr kleinen Bedeckungen Clusterbildung, was auf eine hohe Mobilität und attraktive Wechsel-wirkungen der Kupferatome untereinander schließen läßt. Bei Raumtemperatur erkennt er eine kinetisch kontrollierte dendritische Struktur der Cluster, die sich beim Erhitzen in kompakte Inseln umwandeln (thermodynamische Kontrolle).

Je nach Oberflächenspannung kann das Adsorbat aber auch seine Gitterstruktur ändern. Hahn [HAH94] gibt für Cu/Pd(100) zwei kristalline Phasen an, nämlich fcc (viele kleine irreguläre Inseln) und bct (wenige reguläre Inseln).

Behring [BEH91] beobachtete für das System Cu/Ru(0001) eine Anpassung des Kupfergitters in der ersten Monolage(Pseudomorphie). In der zweiten Lage erfolgt eine laterale Kontraktion in einer Richtung.

2.2 3D-Wachstum

Das dreidimensionale Wachstum auf einer Metalloberfläche läßt sich nach thermody-namischen Betrachtungen grob in drei Wachstumsmoden einteilen [BAU82], [GÜN93]:

• Lage für Lage - Wachstum (Frank - van der Merwe (FM)) [FRA49]
• Lage + Insel - Wachstum (Stranski - Krastanov (SK)) [STR38]
• Insel - Wachstum (Volmer - Weber (VW)) [VOL26]

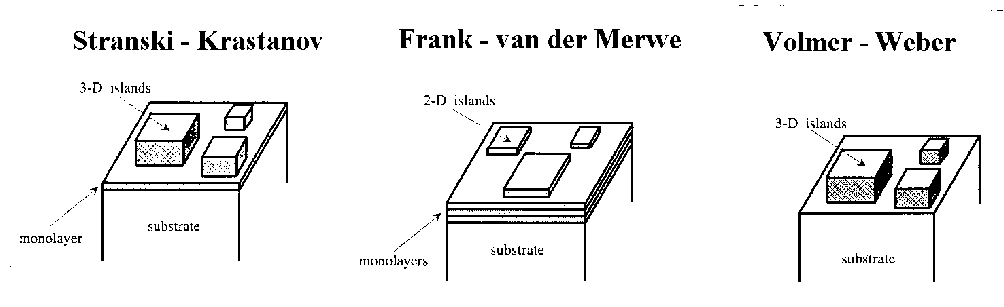
 Abbildung 7 Darstellung der Wachstumsmoden nach [NIC95]

Um diese Moden klassifizieren zu können, werden thermodynamische Eigenschaften der Systeme herangezogen. Dies sind die spezifischen freien Oberflächenenergien des Substrates g_s, des Adsorbates g_a und die Grenzflächenenergie g_i. Diese Grenzfläche ist ein Übergangsgebiet endlicher Dicke zwischen zwei Kristallen mit unterschiedlichen Gittertypen, -konstanten und -orientierungen. g_i enthält also alle chemischen und mechanischen Eigenschaften der Grenzfläche. Nach der einfachen Formel Dg=g_a+g_i-g_s lassen sich die Wachstumsmoden einteilen:

 Dg<0 VW - Wachstum, also starke repulsive Wechselwirkungen und kleine Adsorp-tionsenergie,

Dg³0 SK- oder FM - Wachstum. Der FM - Modus kann nur dann auftreten, wenn die

Beziehung Dg³0 für jede Lage gilt.

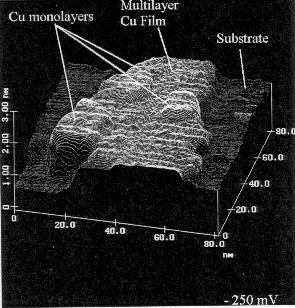
Abbildung 8 FM-Wachstum Cu/Au(111) [NIC95]; Abbildung 9 SK-Wachstum Cu/Au(111) [NIC95]

Abbildung 10 VW-Wachstum Cu/Polypyrrol [NIC95]; Abbildung 11 SK-Wachstum Cu/Ru(0001) [GÜN93]

Beim SK-Wachstum haftet die erste Schicht stark, so daß sie pseudomorph aufwächst. In der zweiten (oder dritten) Lage überwiegen jedoch die Spannungen, und Kristallite bilden sich aus [ARG89].

Günther et al [GÜN93] und Pötschke et al [PÖT91] konnten in STM-Untersuchungen von Cu/Ru(0001) ein SK-Wachstum mit zwei Lagen beobachten, aus denen hexagonale Pyramiden bis zu 10 Lagen entlang der dichtgepackten Richtung der Substratatome wuchsen (s. Abb.11).

Eine Desorption aus Multilagen bzw. Kristalliten ist immer nullter Ordnung [NAG86], weil sich scheinbar die Oberflächenkonzentration nicht ändert. (Die darunter liegenden Atome haben ja den gleichen Zustand wie das desorbierte Atom.)