Energetik und Kinetik des Systems Cu/Re(0001) - Diplomarbeit von Ronald Wagner

3. Meßmethoden

3.1 Thermische Desorptionsspektroskopie (TDS)

3.1.1 Allgemeines

Erstmals wurden Thermodesorptionsspektren (TDS) von Apker im Jahre 1948 [APK48] aufgenommen. Seitdem hat sich an den experimentellen Möglichkeiten, aber auch an den Auswertungsmethoden viel geändert.

Vorangestellt seien einige allgemeine Betrachtungen zur thermischen Desorption eines Teilchens von einer Oberfläche. Das adsorbierte Teilchen befindet sich innerhalb eines Potentials, das es in einem Abstand z_ch zur Oberfläche lokalisiert (vgl. 2.1.1, Abb.1).

Erhält es genügend Energie, so kann es desorbieren. Diese Energie kann dem Adsorbat bei der Thermodesorptionsspektroskopie in Form von Wärme, k_BT, mit einer bestimmten zeitlichen Abhängigkeit (Heizrampe ) b=dT/dt zugeführt werden:

1. : Eine ‘Flash-Desorption’ gibt nur Auskunft über die Anfangsbedeckung, nicht aber über die Kinetik,
2. : Thermodesorptionsspektroskopie (TDS), ,
3. b=0: Isotherme Desorption, direkte Messung der Lebensdauer t möglich.

Auf Grund der Erwärmung desorbieren die Teilchen, und zwar in der Reihenfolge ihrer Bindungsenergie, also die am schwächsten gebundenen zuerst. Dabei sind ein oder mehrere Desorptionsmaxima bei den dazu gehörigen Temperaturen T_max zu beobachten.

Die desorbierten Teilchen werden in einem Massenspektrometer dedektiert und man erhält Spektren der Form p_i=ƒ(t) bzw. p_i=ƒ(T). Wenn das Reaktionssystem schnell genug gepumpt wird, gilt die proportionale Abhängigkeit:

(30)

Durch Integration erhält man die Bedeckung zur entsprechenden Zeit bzw. Temperatur.

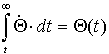(31)

 3.1.2 Spektren mit mehreren Zuständen

Oftmals treten Spektren mit mehreren Zuständen (Multipeakspektren) auf, die man teilweise auf Grund starker Überlappung der einzelnen Zustände nur schwer separieren kann. Sie resultieren aus einer rapiden Veränderung der Desorptionsenergie mit der Bedeckung.

Die Ursache können zum einen starke Wechselwirkungen der Adsorbatteilchen sein. Man erhält dann innerhalb einer Monolage mehrere Peaks, deren Aufspaltung sich mit der Erhöhung der Wechselwirkung vergrößert [ADA74]. Bei größter Aufspaltung sind die Zuständen dabei gleich stark. Allerdings tritt eine solche Aufspaltung eher bei repulsiven als bei attraktiven Wechselwirkungen auf [PAY93], und zwar ab Bedek-kungsgraden, bei denen die Teilchen direkte Nachbarn auf den nächsten Adsorptions-plätzen besitzen.

Zum anderen können Multipeakspektren auch aus Linearkombinationen individueller Peaks zu unabhängigen Bindungszuständen resultieren. In mehrdeutigen Fällen muß hier auf die Monolageneichung durch anderen Meßmethoden, z.B. Augerelektronen-spektroskopie, zurückgegriffen werden.

Die totale Desorptionsrate, die man aus den experimentellen TDS erhält, ist gegeben durch:

(32)

bzw., unter Verwendung der Lebensdauer formuliert:

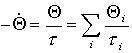(33)

Bei sehr guter Trennung der Peaks kann man diese durch einfache Subtraktion trennen.

Eine weitere Möglichkeit zur Trennung besteht darin, die Peakfläche für den ersten Desorptionszustand zu berechnen und damit alle weiteren Kurven zu simulieren [TAM71]. Eine analytische Auswertungsprozedur nach King [KIN75] vollzieht sich unter Aufnahme von Thermodesorptionsspektren zu verschiedenen Anfangsbedekkungen.

3.1.3 Logarithmische Darstellung der Rate als Funktion der Bedeckung

Eine einfache Möglichkeit, Aussagen über die Desorptionsordnung zu treffen, ist die Verwendung von ‘Orderplots’, einer logarithmischen Darstellung der Rate als Funktion der Bedeckung. Dabei wird vorausgesetzt, daß die Desorptionsenergie und -frequenz unabhängig von der Bedeckung sind [JON90], [NAG86]. Aus der Polanyi-Wigner-Gleichung (10) erhält man, nach Logarithmieren und Umstellen:

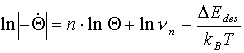(34)

In den Isothermen (lnQ) ist die Desorptionsordnung n direkt als Anstieg gegeben.

 3.1.4 Auswertungsverfahren nach Polanyi

a) Thermodesorptionsspektren nullter Ordnung zeichnen sich durch eine Peakver-schiebung zu höheren Temperaturen aus und besitzen eine gemeinsame Anstiegsflanke. Die Polanyi-Wigner-Gleichung vereinfacht sich zu:

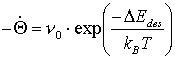(35)

Zudem kann man DE_des und n₀ aus der graphischen Darstellung der logarithmierten Gleichung (35) unter Einbeziehung der Heizrate b als Geradenparameter entnehmen.

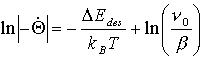(36)

b) Bei einer Desorption erster Ordnung bleibt T_max konstant. Der Bindungsbruch Substrat-Adsorbat ist der langsamste Schritt des Prozesses und damit geschwindigkeitsbestimmend. Ausgehend von der Polanyi-Wigner-Gleichung (10) erhält man, unter Einbeziehung der Heizrate b und der Peakmaximumstemperatur T_max (also ), nach einigen Umformungen

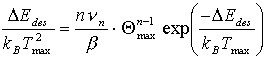(37)

Hier vereinfacht sich wegen n=1 die Beziehung:

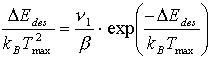(38)

bzw. logarithmiert:

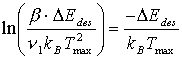(39)

c) Bei der Desorption von Inselrändern können auch gebrochenzahlige Desorptions-ordnungen auftreten. Näherungsweise kann man in diesem Fall

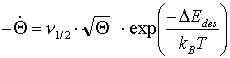(40)

anwenden [CHR91]. DE_des und n_1/2 können auch hier wieder graphisch bestimmt werden.

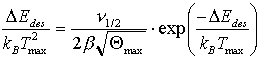(41)

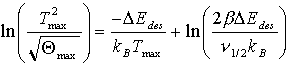und (42)

 3.1.5 Auswertungsverfahren nach Redhead [RED62]

Für Desorptionsspektren erster Ordnung kann die Desorptionsenergie direkt aus Messungen der Temperatur des Peakmaximums erhalten werden.

T_max ist hier bedeckungsgradunabhängig. Daraus ergibt sich eine konstante Desorptionsenergie. Weiterhin wird vorausgesetzt, daß auch der Frequenzfaktor unabhängig von der Bedeckung ist:

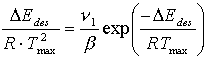(43)

Unter der Nutzung der Beziehung:

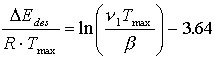(44)

können im Bereich von 10¹³K^-1>n₁/b>10⁸K^-1 Werte für die Desorptionsenergie mit nur 1,5% Ungenauigkeit erhalten werden [RED62]. In der Mehrzahl der Fälle wird n=10¹³s^-1 gesetzt.

 3.1.6 Heizratenvariation

Eine andere Möglichkeit, DE_des zu bestimmen, ist die Messung der heizratenabhängigen Lage des Peakmaximums.

Ausgehend von der Voraussetzung, daß es sich um eine Desorption nullter Ordnung handelt, erhält man die Polanyi-Wigner-Gleichung in der bedeckungsgradunabhängigen Form:

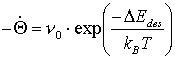(35)

Nach Einführung der Heizrate und unter Ausnutzung der Tatsache, daß die Desorptionsrate sich bei der Peakmaximumstemperatur T_max nicht ändert, kommt man nach einigen Umrechnungen zu:

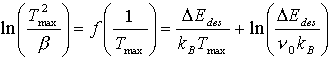(45)

Bei der graphischen Auswertung erhält man eine Gerade, aus deren Anstieg die Desorptionsenergie und aus deren Absolutglied die Desorptionsfrequenz gewonnen werden kann.

Christmann [CHR91] gibt für die Heizratenvariation von Desorptionen erster Ordnung den selben Term an:

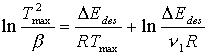(46)

Aus diesem Grunde ist diese Auswertemethode zur Auswertung von Metall-Thermodesorptionsspektren prädestiniert.

3.1.7 Auswertungsverfahren nach King [KIN75]

Die bisher behandelten Auswertungsmethoden können unbrauchbar werden, sobald DE_des oder n bedeckungsgradabhängig sind. Ein Grund dafür können laterale Kräfte zwischen den adsorbierten Teilchen sein. In diesem Fall muß man zu anderen Auswertungsmethoden greifen.

King [KIN75] schlägt ein Verfahren vor, das allein auf der Gültigkeit der Polanyi-Wigner-Gleichung basiert.

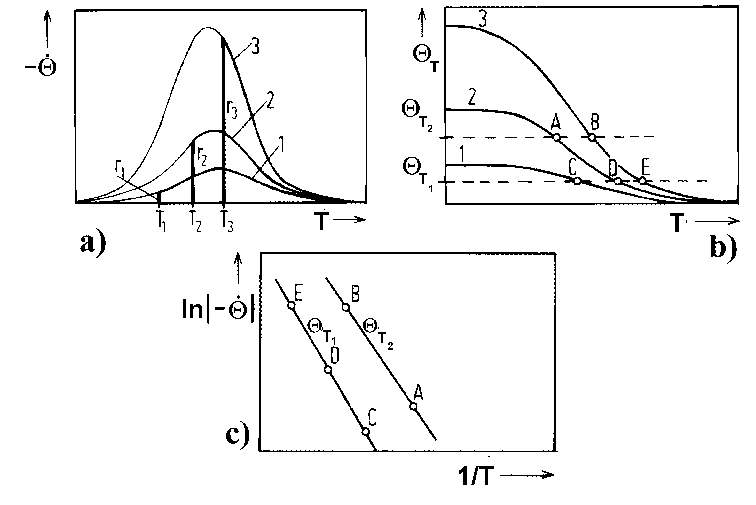
Abbildung 12 Auswertemethode nach King [CHR91]

Hier werden zunächst Serien von Thermodesorptionsspektren zu verschiedenen Anfangsbedeckung Q₀ aufgenommen (s. Abb.12a). Durch die Integration dieser Werte von der Hochtemperaturseite bis zur Temperatur T (Abb.12b) können Wertetripel () gewonnen werden. Mit diesen ist es möglich, Arrheniusplots der allgemeinen Form ln|-dQ/dT|=ƒ(1/T) anzufertigen.

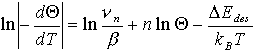(47)

Aus diesen Arrheniusgeraden zu verschiedenen Bedeckungen kann man als Anstieg DE_des(Q) erhalten (Abb. 12c) und, bei bekanntem n, auch n_n(Q) gewinnen.

Wenn die Arrheniusgeraden tatsächlich linear sind, ist der Frequenzfaktor unabhängig von der Bedeckung und als Absolutglied gegeben. Auch n ist dann eindeutig festgelegt.

Wenn die Arrheniusplots nicht linear sind, muß versucht werden, durch Variation von n n_n herauszufinden.

3.1.8 Auswertungsverfahren nach Bauer [BAU75]

Zunächst werden, genau wie beim Verfahren nach King, TDS-Serien (T) aufgenommen. Als zweiter Schritt erfolgt das Integrieren, um zeit- bzw. temperatur-abhängige Bedeckungskurven zu erhalten.

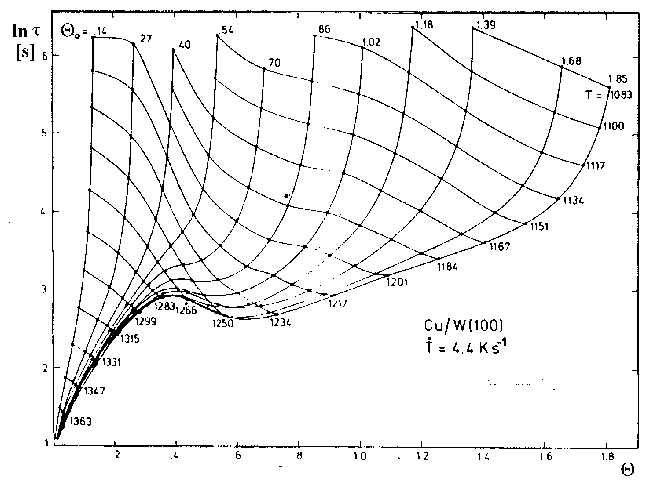
Abbildung 13 Lebensdauer von Cu/W(110) [BAU75]

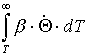
(T) (48)

Aus den Wertepaaren (Q; -)ist es möglich, die Lebensdauer zu berechnen.

t(Q, T) (49)

In einer Darstellung lnt=ƒ(Q) kann man die Punkte gleicher Temperaturen zu einem Satz von ‘Isothermen’ zusammenfassen (s. Abb.13).

Aus den Isothermen ist die Temperaturabhängigkeit der Lebensdauer zu festen Bedeckungen ersichtlich. Durch Logarithmieren von (7) erhält man:

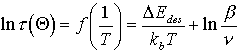(50)

In diesen isosteren Arrheniusplots sind die Werte für DE_des und n als Geradenparameter gegeben. Wenn sich die Kurven in der Arrheniusauftragung nicht durch einheitliche Geraden darstellen lassen, kann das mehrere Ursachen haben:

• das Vorhandensein von mehr als einem Adsorptionsplatz,
• Desorption nicht aus dem Quasi-Gleichgewicht,
• das Auftreten von Quanteneffekten, die eine Temperaturabhängigkeit von n bedingen können (Physisorptionszustände),
• ein Phasenübergang vom 2D-Gas in die 2D-Gas/Kondensat-Koexistenzregion.

Besonders im Submonolagenbereich erhält man die beste Übereinstimmung durch das Zuordnen von zwei Arrheniusgeraden, eine im Bereich sehr kleiner Bedeckungen für den Zustand des 2D-Gases und eine für die 2D-Gas-Kondensat-Koexistenzregion bei höheren Bedeckungen [BAU87].

Alternativ ist auch die Berechnung der Arrheniusgeraden über einen anderen Ausdruck möglich, der sich zwanglos durch das Einsetzen von (7) in (26) und wenige rechnerische Umformungen ergibt:

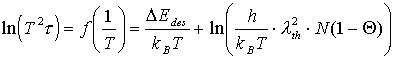(51)

Die so berechneten Thermodesorptionsspektren stimmen mit den gemessenen besser überein, jedoch unterscheiden sich die Werte von DE_des und n nicht sehr stark von denen über (50) berechneten [BAU75].

3.1.9 Auswertungsverfahren nach Habenschaden und Küppers [HAB83]

Bei der Auswertung nach Habenschaden und Küppers geht man von der logarithmierten Form der Polanyi-Wigner-Gleichung (36) aus. Direkt aus der Arrheniusauftragung wird hier die Desorptionsenergie mit einer für diese an sich einfache Methode doch beachtlichen Genauigkeit entnommen. Eine Abhängigkeit der Desorptionsenergie von der Bedeckung, dem Frequenzfaktor und der Desorptionsordnung kann vernachlässigt werden, wenn die Thermodesorptionsspektren nur im ersten kleinen Teil des Anstieges auf der Niedertemperaturseite (ca. 4% [HAB83]) untersucht werden.

Diese Methode stellt eine sehr direkte Art der Auswertung von Thermodesorptions-spektren dar, weshalb man mit ihr besonders gut Systeme untersuchen kann, die sich nicht im Gleichgewicht befinden.

 3.1.10 Weitere Effekte

Bei konventionellen Auswertemethoden von Thermodesorptionsspektren z.B. nach Redhaed, wo eine konstante Temperatur des Peakmaximums vorausgesetzt wird, bestand die Schwierigkeit in der Deutung der Veränderung der Maximumstemperatur (Peakverschiebung) mit der Bedeckung.

Die Peakverschiebungen können auf zwei Weisen erklärt werden:

1. laterale Wechselwirkungen innerhalb des Adsorbats,
2. Precursorzustände: schwach gebundene (physisorbierte) Zustände, die den Teilchen erlauben, einen freien Adsorptionsplatz zu erreichen [CHR91], [KIN75].

Nagai formuliert unter Bezug auf die Molekularfeldnäherung (MFA) [NAG86] für die Desorptionsrate:

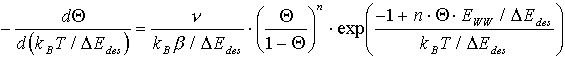(52)

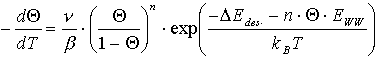bzw. (53)

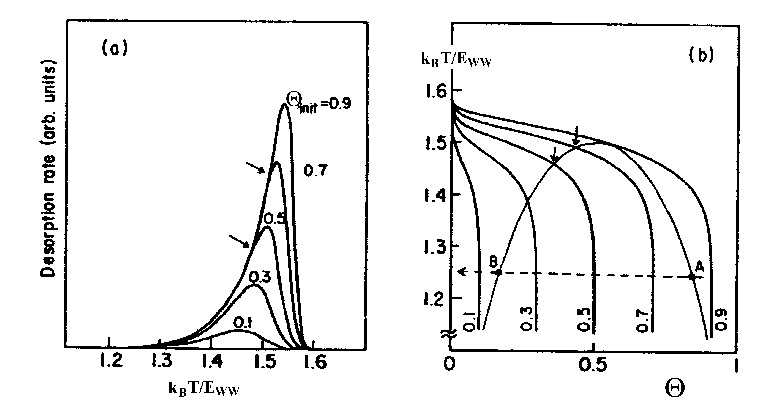
Abbildung 14 a) TDS und b) T=f(Q) als Desorptionslinien im Phasendiagramm [NAG86]

Eingezeichnet im Phasendiagramm sind die Desorptionslinien der Thermodesorptions-spektren. Die Pfeile markieren den Übergang von der Desorption 0. Ordnung zu quasi 1. Ordnung. Im TDS sind das die Punkte, an denen der gemeinsame Anstieg endet und die Spektren auseinanderlaufen.

Bei der Thermodesorption erster Ordnung konnte von Nagai [NAG86] eine Verschie-bung der Maximumstemperatur durch die Berücksichtigung der internen Wechselwirkung erzwungen werden:

• -0,1£E_ww/DE_des<0: Verschiebung zu höheren Temperaturen, starke attraktive Wech-selwirkung, gemeinsame Anstiegskante,
• 0,1³E_ww/DE_des>0: Verschiebung zu tieferen Temperaturen, starke repulsive Wech-selwirkung,
• E_ww/DE_des=0: keine Verschiebung, keine Wechselwirkung.

3.2 Augerelektronenspektroskopie (AES)

3.2.1 Allgemeines

In den Jahren 1922 - 1925 studierte Pierre Auger den Photoeffekt bei Experimenten mit der Nebelkammer. Nach der Bestrahlung von Atomen mit Röntgenstrahlen registrierte er neben den Photoelektronen weitere Elektronen, deren Energie durch die Differenz der Energieniveaus der bestrahlten Atome bestimmt war. Diese emittierten Elektronen werden Augerelektronen genannt. Lander konnte 1953 Augerelektronen auch nach dem Beschuß einer Materialoberfläche mit Elektronen nachweisen.

Die Augerelektronenspektroskopie (AES) wird heute als oberflächenempfindliche chemische Analysenmethode auf ein weites Feld von Problemen angewendet. Sie liefert reproduzierbare Aussagen an chemisch homogenen, ebenen, ein- und polykristallinen Oberflächen.

3.2.2 Der Augerprozeß

Wird ein Elektron infolge einer Energiezufuhr, etwa durch das Einstrahlen einer elektromagnetischen Welle oder den Beschuß mit Elektronen, aus seinem Atomverband völlig entfernt, so handelt es sich hierbei um den Vorgang der Ionisation. Erfolgt die Ionisation durch elektromagnetische Strahlung, so wird dieser Vorgang Photoeffekt und das emittierte Elektron Photoelektron genannt.

Der Augerprozeß wird durch den Stoß von sogenannten primären Elektronen eingeleitet. Ein (sekundäres) Elektron in Kernnähe wird dabei herausgeschlagen und es entsteht ein einfach positiv geladenes Ion. Die zurückbleibende Defektstelle wird durch ein Elektron eines höheren Energieniveaus wieder aufgefüllt. Dabei wird Energie frei, die auf ein weiteres (Auger-) Elektron übertragen wird und so groß ist, daß dieses nun auch emittiert wird (interner Photoeffekt). Es entsteht ein zweifach positiv geladenes Ion.

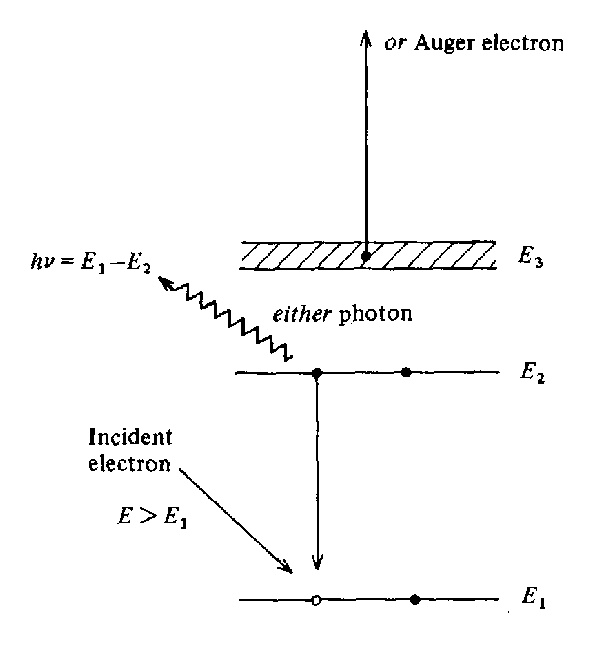
Abbildung 15 Der Augerprozess [BIS89]

Weiterhin muß das austretende Elektron die Austrittsarbeit des entsprechenden Substrates überwinden. Die kinetische Energie des Augerelektrons berechnet sich in erster Näherung nach:

E_kin=E₁-E₂-E₃-F_S (54)

Dabei ist E₁ die Bindungsenergie im Bindungsniveau W, aus dem ein sekundäres Elektron herausgeschlagen wurde. E₂ ist die Bindungsenergie des Elektrons im Bindungsniveau X, aus welchem das Elektron in die freie Stelle fällt und E₃ die Bindungsenergie des Augerelektrons aus dem Bindungsniveau Y. Ein solcher Augereffekt wird mit WXY bezeichnet. Zur Bezeichnung eines konkreten Überganges werden die röntgenographischen Bezeichnungen für die Atomenergieniveaus und deren Unterniveaus als Index benutzt (K für das 1s-Orbital, L₁ für das 2s-, L₂ und L₃ für die 2p-Orbitale usw.).

Die Anzahl der Linien im Augerspektrum wird durch die möglichen Übergänge bestimmt, die sich wiederum aus der Kopplung der Bahn- und Spindrehimpulse der beteiligten Elektronen ergeben. Der Prozeß ist eine rein elektrostatische Wechselwir-kung der umgebenden Elektronenwolke mit dem Kernloch W, so daß keine Auswahl-regeln wie bei optischen Übergängen limitierend wirken.

Die bisher vorgenommenen Betrachtungen beziehen sich auf Atome im Gaszustand. Im Festkörper ist die Situation durch die Ausbildung von Leitungs- und Valenzbändern mit einer bestimmten Energiebandbreite (hier V genannt) anders. Hier wird die kinetische Energie der Augerelektronen um den Betrag der "extraatomaren Relaxationsenergie" E_Rel geändert [GRA85]. Nach der Ionisation eines inneren Niveaus W eines Atoms im Festkörper ergibt sich eine völlig geänderte Anordnung im Valenzband V und rückwirkend auch eine Änderung der Elektronenverteilung in den inneren Niveaus. Außerdem ist die Augerlinie von Atomen im Festkörper im allgemeinen breiter und hat einen Ausläufer zu geringeren Energien hin. Gleichung (54) muß also neu (genauer) formuliert werden:

E_kin=E₁-E₂-E₃-F_S +E_Rel (55)

Die energetischen Aspekte beim Augerprozess im Festkörper (jetzt WVV statt bisher WXY) werden aus Abb.16 ersichtlich.

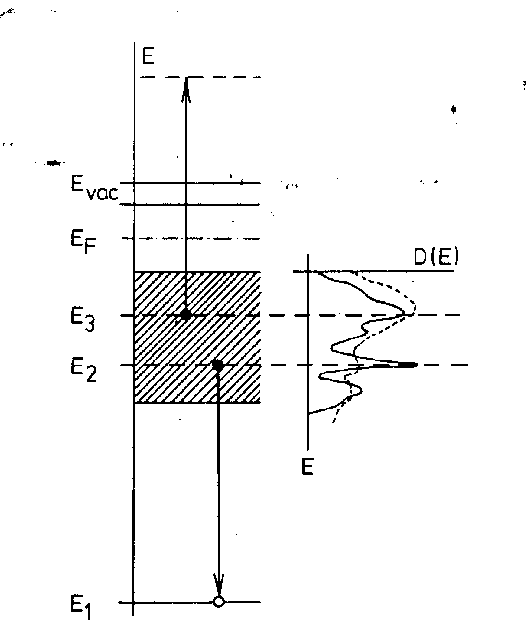
Abbildung 16 Augerübergänge im Festkörper [CHA71]

Ein wichtiger Aspekt im Augerprozess ist die Energie der anregenden primären Elektronen. Auf die Lage der Augerlinien hat sie zwar keinen Einfluß, wohl jedoch auf den Ionisierungsquerschnitt. Zu kleine Primärenergien können die Ionisation nicht initiieren, bei zu großen Energien hat das Primärelektron auf Grund seiner Geschwindigkeit keine Zeit, um Wechselwirkungen einzugehen. Chang [CHA71] gibt als Faustregel für die optimale Ionisierungsenergie an. Die sich dabei ergebende Augerelektronendichte beträgt .

Konkurrierend zur Aussendung eines Augerelektrons kann die frei werdende Energie auch als Röntgenstrahlung emittiert werden. Bei Elementen mit Massenzahlen Z<32 (Ge) überwiegt der Augerprozeß. Burhop [BUR55] gibt zur Abschätzung des Anteiles des Augerprozesse folgende Formel an:

(56)

Für Kupfer ergibt sich ein Wert von 60,7% und für Rhenium von 1,36%.

 3.2.3 Messung der Energieverteilung der Elektronen - Das direkte Spektrum

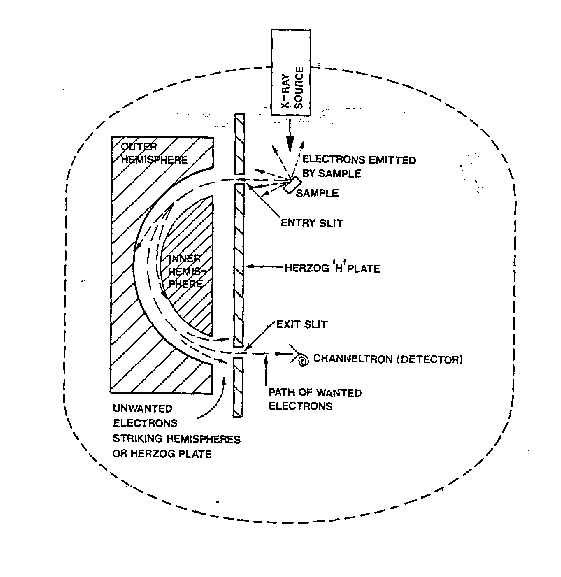
Abbildung 17 Konzentrischer Henisphärenanalysator

Charakteristisches Merkmal der Augerelektronen und damit auch der emittierenden Atomart ist deren Energie. In einem Elektronenspektrometer, hier ein CHA (concentric hemisphere analyser) gelangen die Elektronen auf Grund ihrer kinetischen Energie durch ein Linsensystem zwischen zwei Halbschalen (Hemisphären), zwischen denen sich ein elektrisches Feld befindet. Durch dieses Feld werden die Elektronen so in ihrer Bewegung beeinflußt, daß nur solche mit einer bestimmten Energie den nachge-schalteten Elektronenvervielfacher erreichen. Der CHA ist durch seine beiden Hemi-sphären doppelt fokussierend [ERT74].

Es wird eine ‘Bremsspannung’ (retarding Field) vorgeschaltet, um damit selektiv nur Elektronen mit einer bestimmten Mindestenergie durchzulassen. Durch Verände-rung der Feldstärke zwischen den beiden Hemisphären mittels einer Modulationsfre-quenz können schließlich Elektronen mit einer ganz bestimmten Energie (-bandbreite) ausgewählt werden. Der Verlauf der Intensität der Elektronen in Abhängigkeit von der Energie wird direktes Spektrum genannt. Der in Gleichung (55) eingeführte Term der Austrittsarbeit des Substrats muß hier durch die Austrittsarbeit des Elektronenspektro-meters ersetzt werden, solange Probe und Analysator auf gleichem Potential liegen (bzw. zwischen ihnen die Spannung des Bremsfeldes liegt).

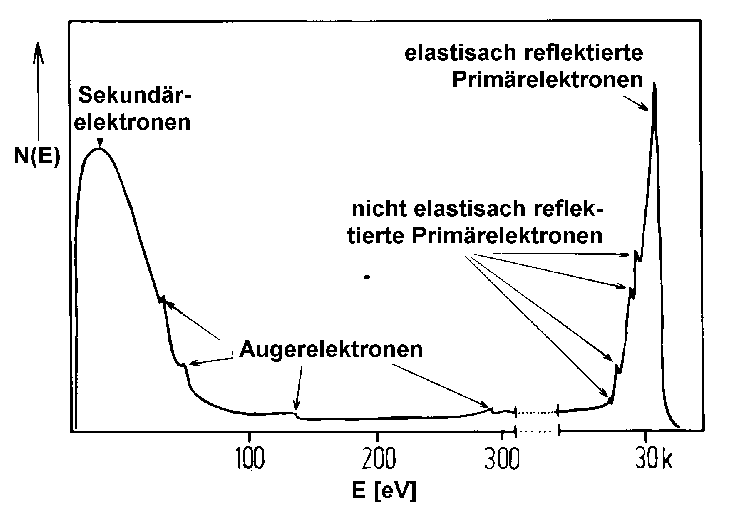
Abbildung 18 Direktes Augerspektrum (E_prim=30keV) [CHR91]

Im niederenergetischen Teil des Spektrums werden die sekundären (W-) Elektronen abgebildet, und zwar besonders scharf und stark, weil durch die Kollisionen der Primärelektronen im Festkörper eine Kaskade von Sekundärelektronen entsteht [CHA71]. Bei E=E_prim sind die elastisch reflektierten Primärelektronen zu erkennen. An der niederenergetischen Seite dieses Signals befinden sich kleine Peaks, die von nicht elastisch reflektierten Elektronen stammen. Im mittleren Bereich des Spektrums, auf dem Untergrund weiterer inelastisch gestreuter Elektronen, werden die eigentlichen Augerelektronen abgebildet.

 3.2.4 Das differenzierte Spektrum

Häufig sind die Augersignale sehr klein gegenüber den anderen Beiträgen des Spektrums. Ein wesentlicher Fortschritt beim Nachweis der Augerlinien kann durch elektronisches Differenzieren (nach der Energie) erzielt werden. Hierbei wird der niederfrequente Untergrund und ein Teil des Rauschens unterdrückt und die Augerlinien stark hervorgehoben. Die Differentiation wird mit Hilfe eines Lock-in-Verstärkers vorgenommen, der noch einen weiteren wichtigen Vorteil bietet. Auf die Hemisphären-spannung (vgl. 3.2.1) wird eine Wechselniederspannung aufmoduliert, die die Bandbreite des CHA bestimmt. Das so modulierte Signal wird vom Lock-in-Verstärker, im Vergleich mit der angelegten Referenz, frequenzselektiv erkannt und von den restlichen Signalen getrennt.

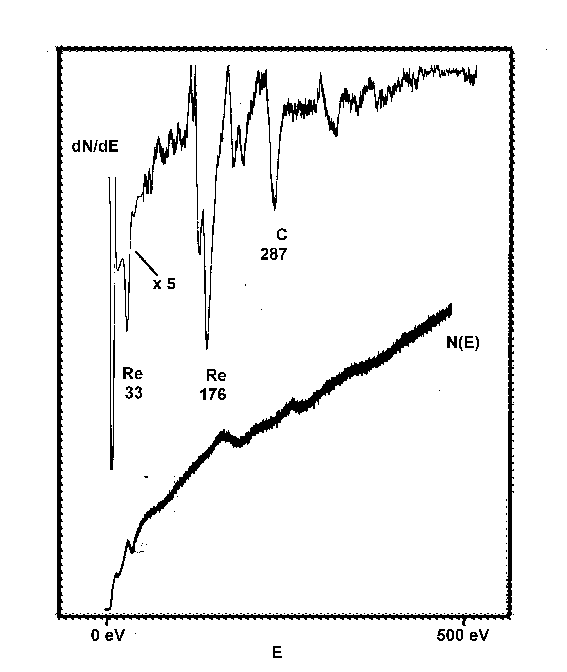
Abbildung 19 direktes und differenziertes Augerspektrum, gemessen mit einem CHA

3.2.5 Quantitative Messung

Wie auch bei anderen Verfahren der Mikrobereichsanalyse werden bei der quantitativen AES-Analyse nicht absolute Intensitäten, sondern nur Intensitätsverhältnisse gemessen. Im differenzierten Spektrum werden die Augerintensitäten durch das Ausmessen des Abstandes zwischen dem niederenergetischen Maximum und dem höherenergetischen Minimum ermittelt.

Bei einer Gaußverteilung der Intensität des Augerpeaks ist der Max-Min-Abstand im differenzierten Spektrum bis auf einen Faktor gleich der Intensität im N(E)-Spektrum [ARG89]. Auch für einen nicht symmetrischen Verlauf eines Zustandes bzw. einer Überlagerung zweier Zustände kann (bei kleiner Modulationsfrequenz) nach Grasser-bauer [GRA85] immer noch von einem linearen Zusammenhang zwischen dem Max-Min-Abstand und der Intensität im N(E)-Spektrum ausgegangen werden.

Im Bereich der Sekundärelektronenemission ändert sich der Untergrund im N(E)-Spektrum sehr schnell. Deswegen ist auch ein Einfluß auf die Signalintensität zu erwarten.

3.2.6 Auswertungsmethoden

Die quantitative Augerelektronenspektroskopie kann genutzt werden, um den Bedek-kungsgrad eines Substrats zu bestimmen. Man bedient sich hierbei des Umstandes, daß die Augerelektronenspektroskopie recht oberflächenempfindlich ist (vgl. 3.2.7) und das Signal des Substrats mit steigender Bedeckung abgeschwächt wird. Ebenso nimmt das Signal des Adsorbats zu. Aus der Darstellung dN/dE=ƒ(Q) lassen sich darüber hinaus Rückschlüsse auf das Wachstumsverhalten des Adsorbats ziehen.

Dabei ist zu beachten, daß das Signal des Substrats im Bereich kleiner Bedeckungen sensitiver ist als das des Adsorbats, weil es auf Grund der hier größeren Oberflächen-konzentration stärker ist und damit ein besseres Signal-zu-Rausch-Verhältnis besitzt. Das Signal des Adsorbats hingegen ist bei höheren Bedeckungen das empfindlichere. Außerdem sind die Signale dann besonders aussagekräftig, wenn ein Adsorbatpeak hoher Energie und ein Substratpeak kleiner Energie gewählt wird [BIB79].

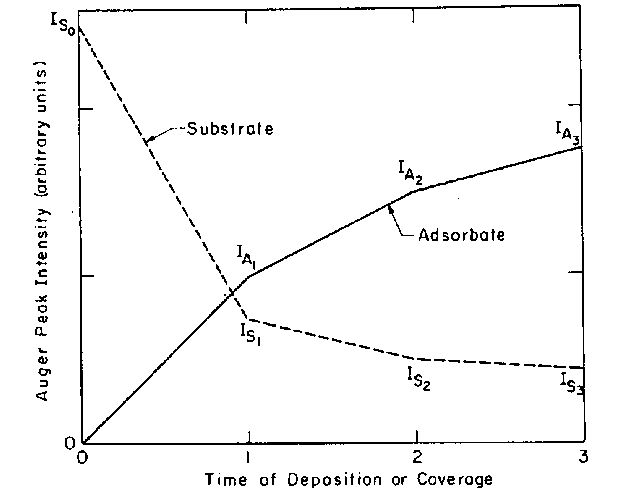
Abbildung 20 Schematisierter Verlauf der AES-Intensitäten [BIB79]

Nimmt man für den Haftkoeffizienten S=1 an (jedes auftreffende Adsorbatteilchen bleibt haften), wird die Aufdampfzeit proportional zur Bedeckung. Ist das nicht der Fall, kann es passieren, daß Feinheiten im Kurvenverlauf nicht zu erkennen sind.

Die in Abb.20 auftretenden Steigungsbrüche kennzeichnen meistens die Auffüllung einer Monolage des Adsorbats. Eine Auflösungsverbesserung kann durch die Darstel-lung I_s=ƒ(I_a) oder I_S/I_A=ƒ(Q) erreicht werden.

Anhand der Kurvenform (Anzahl der Knicke) kann man Rückschlüsse auf den Wachstumsmodus des Adsorbats (vgl. 2.2) ziehen:

• kein Knick: Vollmer-Weber-Wachstum,
• ein Knick: Stranski-Krastanov-Wachstum,
• mehr als ein Knick: Frank-van der Merwe-Wachstum.

Es ist hierbei entscheidend, ob das Augerelektron eine, bzw. mehrere geschlossene Lagen durchdringen muß oder ob es die Möglichkeit hat, sich zwischen Kristalliten zu bewegen.

 3.2.7 AES Informationstiefe

Da zum Signal im Augerelektronenspektrum nur diejenigen Elektronen beitragen, die noch keine Energie an Festkörperatome abgegeben haben, ist für die Informationstiefe der Augerelektronenspektroskopie daher die mittlere freie Weglänge der Augerelek-tronen entscheidend (Weg zwischen Entstehungsort und dem ersten unelastischem Stoß (IMPF)). Diese Länge ist energieabhängig und hat für 20eV bis 100eV eine Größenordnung des 0,4- bis 3-fachen eines Atomdurchmessers, für 1keV des acht-fachen Atomdurchmessers [BIS89].

Das Verhältnis der Intensitäten von Adsorbat und Substrat I_A/I_S an Knicken ist charakteristisch für die jeweilige Monolage. Es lassen sich aus den Intensitätsverhält-nissen die Durchdringungskoeffizienten bestimmen.

a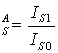 (57)

Daraus wiederum läßt sich daher die mittlere freie Weglänge der Augerelektronen l berechnen:

(58)

Zur Erhöhung der Oberflächenempfindlichkeit kann mit streifendem Einfall der Primärelektronen gearbeitet werden [CHR91].