Energetik und Kinetik des Systems Cu/Re(0001) - Diplomarbeit von Ronald Wagner

 Im folgenden Teil III wird beschrieben, wie die aufgenommenen Daten weiterver-arbeitet und bestimmten Auswertungsmethoden unterzogen wurden. Dabei werden thermodynamische und kinetische Größen erhalten sowie Aussagen über das Wachs-tumsverhalten des Systems gemacht.

Teil III gliedert sich in drei Kapitel. Kapitel 1 widmet sich der Bearbeitung der Thermodesorptionsspektren und Kapitel 2 der Auswertung der Augerelektronenspek-tren. In Kapitel 3 schließlich werden einige weiterreichende Betrachtungen besonders über das Verhalten der Teilchen innerhalb der ersten Lage ausgeführt.

1. Auswertung der Thermodesorptionsspektren

Zunächst wird beschrieben, wie die aus den Messungen erhaltenen Rohspektren bearbeitet wurden, um eine Basis für die weiteren Untersuchungen zu schaffen.

Danach wird die Form der Spektren einer Analyse unterworfen, um Informationen über die Anzahl und die Lage der Desorptionszustände zu erhalten. Um die Betrachtungen so genau wie möglich zu gestalten, werden mehrere Thermodesorptionsserien ent-sprechend den verschiedenen Fragestellungen untersucht.

Diese Betrachtungen werden in Unterkapitel 3 weitergeführt, hier allerdings vornehm-lich, um Aussagen über die Desorptionsordnung treffen zu können. Zum selben Zweck wird die Anfertigung und Auswertung von ‘Orderplots’ beschrieben.

Ein nächster ausführlicher Abschnitt widmet sich der Anwendung der verschiedenen Auswertungsmethoden für die Desorptionsenergie. Die Rechnungen werden an ver-schiedenen Meßserien ausgeführt. Als Ergebnis können die einzelnen Methoden hinsichtlich ihrer Genauigkeit und Handhabbarkeit bewertet sowie die Desorptions-energie und der Frequenzfaktor der Desorption relativ exakt bestimmt werden.

1.1 Aufbereitung der Meßdaten

1.1.1 Bearbeitung der Rohspektren

Ziel einer guten Anpassung ist es nicht, die eigene ‘Unfähigkeit beim Messen’ zu vertuschen. Vielmehr kommt es darauf an, Effekte, die ‘im dunklen Untergrund des Rauschens schlummern’ oder sich ‘dem Auge des Betrachters durch Unscheinbarkeit’ entziehen, sichtbar zu machen und hervorzuheben.

Schon während der Messungen wurden die aufgenommenen Daten bearbeitet. Wie unter II.4 beschrieben, sind die extrahierten Werte bereits Mittelungen von über ca. 50 Einzelmessungen.

Außerdem wurden die Meßdaten direkt in den Rechner eingelesen, wodurch die enorme Datenfülle (ca. 1000 Wertepaare pro Spektrum!) erst handhabbar wurde. Pro Serie wurden 20 bis 60 Spektren aufgenommen. Diejenigen Spektren, die sich wegen zufälliger Störeinflüsse nicht in die Serie einfügten, sind vernachlässigt worden.

Von allen Rohspektren wurde zunächst der Untergrund subtrahiert. Das geschah pauschal, indem die Werte der Grundlinie vor und nach der Desorption jeweils gemittelt wurden. Die Verbindungslinie dieser beiden Mittelwerte wurde als Grundlinie (Offset) vom Rohspektrum subtrahiert. Geglättet wurden alle so erhaltenen Spektren mittels einer Fouriertransformation Abtrennung aller Frequenzen, die größer waren als eine maximale berücksichtigte Frequenz, was der Wirkung eines Tiefpassfilters entspricht.

Die einzige Ausnahme bildete die Serie 9, bei der diese Methode unbefriedigende Ergebnisse lieferte. Grund dafür sind die sehr kleinen Intensitäten der Spektren. Eine Glättung wurde hier durch die Anpassung an eine Lorenzfunktion vorgenommen. Die Übereinstimmung ist überzeugend, lediglich im letzten Teil des Desorptionszustandes (ca. 1 bis 2%) ist die Flanke der Rohspektren steiler als die der Lorenzkurven.

Geglättet wurden allgemein alle Endergebnisse, soweit dies nötig war; alle Zwischen-ergebnisse wurden jedoch ungeglättet weiterverwendet, damit keine Information verloren gehen konnte.

Die ebenfalls eingelesenen Werte der Thermospannung (Temperaturkontrolle des Substrates) sind auf die Werte einer Wertetabelle extrapoliert worden, die die Thermospannungen in Schritten von 0.1mV (10°C) enthält. Die so erhaltenen Werte wurden in Kelvin umgerechnet.

 1.1.2 Monolageneichung

Aus Gleichung (30) geht hervor, daß es sich bei der Aufnahme der Thermodesorp-tionsspektren nicht um eine Messung der Absolutwerte für die Bedeckungs-gradänderung bzw. Desorptionsrate handelte, sondern nur der Relativwerte.

Die Eichung der Ergebnisse auf den Bedeckungsgrad geschah folgendermaßen. Für jede Spektrenserie wurde die Desorptionsrate über dem relativen Bedeckungsgrad aufgetragen, der durch Integration der Thermodesorptionsspektren errechnet worden war (s. Abb.30). Die Ausbildung der einzelnen Desorptionszustände ist auch hier deutlich an den Maxima der Spektren zu erkennen. Dabei gehören alle Spektren mit nur einem Maximum zum b₃-Zustand. Der Schnittpunkt desjenigen Spektrums des b₃-Zustandes mit der Bedeckungsachse, das das höchste Maximum hat, kennzeichnet den Normierwert der ersten Monolage. Durch diesen Wert sind alle Bedeckungswerte der betreffenden Serie geteilt worden. (In Abb.30 ist dies natürlich der Wert 1, da die abgebildeten Spektren bereits normiert sind.)

1.2 Kurvenformanalyse

Abb.29 zeigt die Thermodesorptionsspektren aus Serie 1 (Tab.3). Abgebildet sind hier Spektren bis zu einer Anfangsbedeckung von 20 Monolagen.

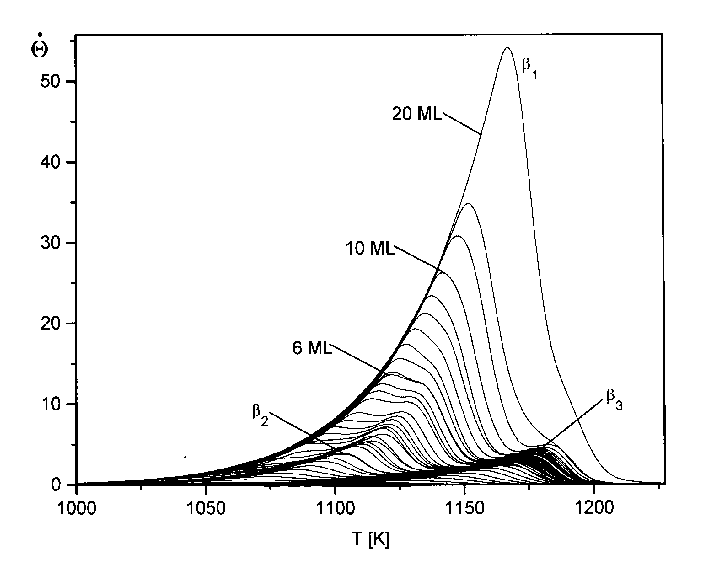
 Abbildung 29 Thermodesorptionsspektren der Serie 1 (s. Tab.3) J_ads=570°C; b=4,1K/s

Es sind deutlich drei Desorptionszustände zu erkennen, b₁, b₂ und b₃. Der b₃-Zustand bildet sich (bei der gewählten Heizrate von 4,1K/s) ab T=1100K aus und hat sein Maximum (Q=1ML) bei T=1170K. Der b₂-Zustand entwickelt sich bei T=1033K und hat ein Maximum (Q=2ML) bei T=1103K. Der dritte Zustand, b₁, beginnt bei T=1000K und hat ein Maximum (Q=3ML) bei T=1083K. Dieser Zustand gewinnt mit zunehmender Anfangsbedeckung sehr stark an Größe, so daß er, bei einer Anfangsbedeckung von etwa Q₀=10ML den b₂-Zustand überdeckt und, bei Q₀=20ML, auch den b₃-Zustand. Der b₁-Zustand und der b₂-Zustand liegen etwa im gleichen Temperaturbereich der Niedertemperaturseite des Spektrums, jedoch in größerer Entfernung zum b₃-Zustand. Das weist bereits darauf hin, daß der b₁- und der b₂-Zustand energetisch ähnlich sind. In den Arbeiten von He et al [HEG90] und Rodgriguez et al [ROD91] sind nur der b₁ und der b₃- Zustand zu erkennen, ein Umstand, der durch eine schlechtere Auflösung bei den Messungen zu erklären ist.

Durch eine Veränderung der Heizrate b ändern sich nicht nur die Maximums-temperaturen der Zustände, sondern auch die Auflösung und die Intensität der Spektren. Ein Anstieg von b führt zur Erhöhung der Intensität, da in einer Zeiteinheit mehr Teilchen desorbieren, jedoch nur ein konstanter Teil von der Pumpe des UHV-Systems abgesaugt wird. Die Auflösung verschlechtert sich aber gleichzeitig, ein Effekt, der bei vielen Prozessen beobachtet werden kann. Die höchste Auflösung erhält man bei kleiner Heizrate. Wird sie jedoch zu klein gewählt, verschwindet das Signal schließlich im Untergrund. Die Wahl der richtigen Heizrate ist also abhängig von der Intensität des Signals und der Aufspaltung der Zustände.

Zur Untersuchung weiterer möglicher Desorptionszustände auf der Niedertempera-turseite wurde Serie 3 (Abb.30a) gemessen. Die Heizrate ist hier bewußt sehr klein gewählt worden (b=2,1K/s), um eine größtmögliche Auflösung zu erreichen.

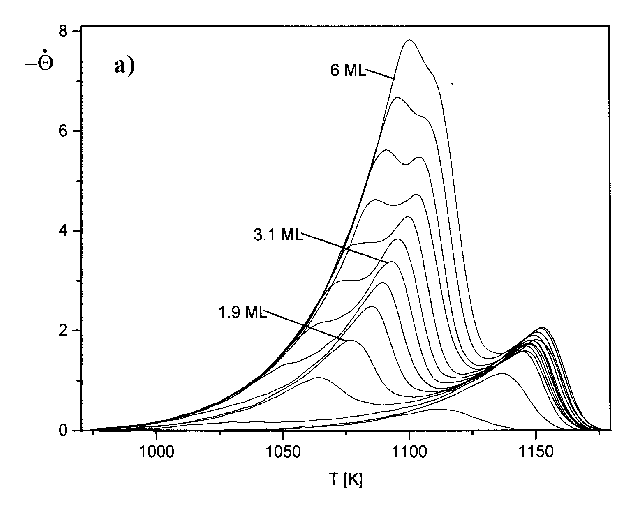
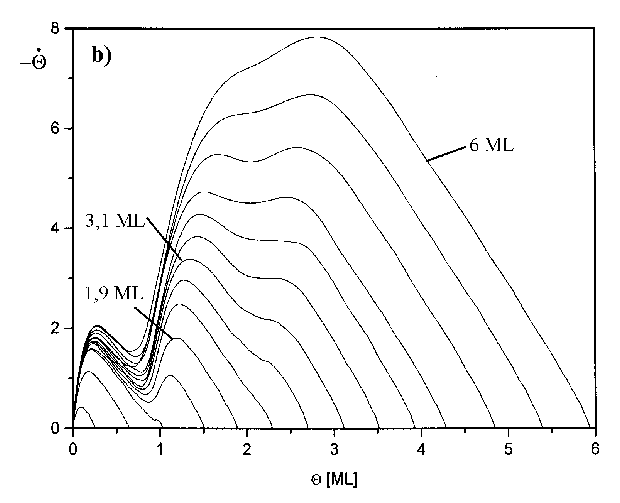
 Abbildung 30 a) TD-Spektren der Serie 3 (s. Tab.3) J_ads=690°C; b=2,1K/s, b) Auftragung Rate vs. Bedeckung für Spektren der Serie 3 (s. Tab.3)

In Abb.30b ist die Auftragung der Rate vs. Bedeckung dargestellt. Zu einer solchen Darstellung gelangt man, indem man die Thermodesorptionsspektren von der Hochtemperaturseite her integriert, um die Bedeckung des Substrates während der Desorption zu erhalten (s. Abb.38) und für jedes TD-Spektrum die Desorptionsrate gegen die so gewonnene Bedeckung darstellt. Von rechts nach links kann man für die einzelnen Anfangsbedeckungen Q₀ den Verlauf der Desorptionsrate mit der Bedeckung verfolgen.

Besonderes Augenmerk galt der Ausbildung eines eventuellen vierten Peaks beim Übergang zur vierten Monolage. Die Flanken der Spektren zeigen jedoch keine Schultern oder gar neue Maxima, was darauf schließen läßt, daß sich die Ausbildung einer weiteren Lage nicht als neuer Zustand in diesem Gebiet dokumentiert. In Untersuchungen des Systems Ag/Re(0001), die unter gleichen Bedingungen und an der gleichen Apparatur ausgeführt wurden, waren durchaus Unregelmäßigkeiten in der betrachteten Flanke zu erkennen [SCH97].

Da der Verlauf der Spektren für sehr kleine Bedeckungen aus den Abb.29 und 30 nicht genau zu erkennen ist, wurde eine weitere Spektrenserie (Serie 9) aufgenommen. Es ist hier eine relativ hohe Heizrate gewählt worden (b=21,7K/s), da im Bereich dieser kleinen Anfangsbedeckungen die Intensität der Zustände sehr gering ist.

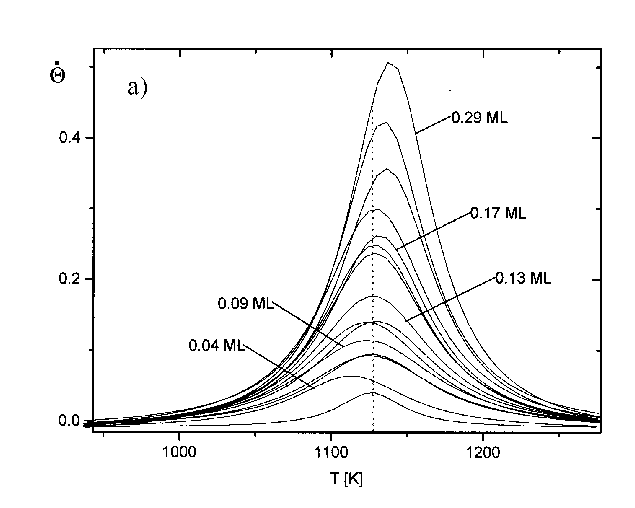
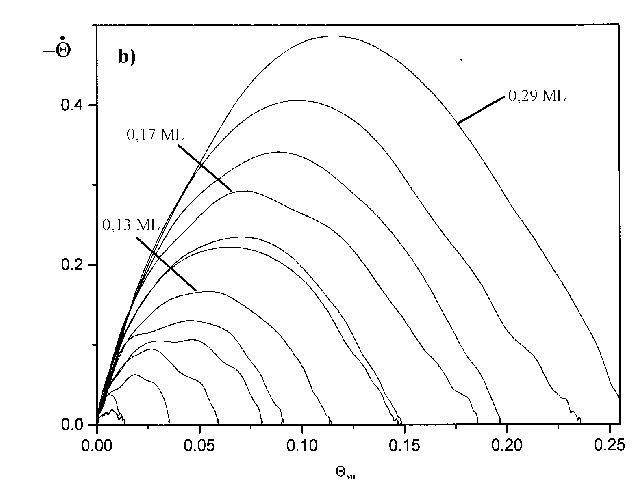
Abbildung 31 a) TD-Spektren der Serie 9 (s. Tab.3) J_ads=390°C; b=7,7K/s, b) Auftragung Rate vs. Bedeckung für Spektren der Serie 9

Die Ausbildung eines weiteren Zustandes ist auch hier nicht zu erkennen. Ein anderer Fakt wird aber deutlich. Entgegen dem Verhalten der Desorptionsspektren zu höheren Anfangsbedeckungen verändert sich hier die Maximumstemperatur nicht. Für alle Spektren bis Q₀=0,15ML wird bei der gewählten Heizrate der Wert T_max=1127K erhalten. Dieser Umstand soll im nächsten Absatz und unter 1.4.1 erläutert werden.

 1.3 Untersuchung der Desorptionsordnung

1.3.1 TDS-Serienanalyse

Wie aus Abb.29 zu erkennen ist, fallen die Anstiegsflanken gleicher Zustände aller Spektren (zu unterschiedlichen Anfangsbedeckungen) zusammen. Dies ist besonders gut beim b₁-Zustand ersichtlich. Die Niedertemperaturflanken aller Spektren bilden bis zur Temperatur T_g eine gemeinsame Linie. Danach wird der Anstieg der individuellen Spektren kleiner, und sie verlassen die Flanke. Nach dem Passieren des Maximums bei T_max laufen sie gegen null.

Dieser Effekt der ‘gemeinsamen Anstiegsflanke’ ist kennzeichnend für eine Desorption nullter Ordnung [NAG86], [NAG91], [CHR91]. Nagai beschreibt allerdings auch weiter, daß durch laterale Wechselwirkungen solche Effekte vorgetäuscht werden können, etwa durch starke attraktive Wechselwirkungen zwischen den Adsorbatteilchen. Nichtsdestoweniger ist die vorliegende Kurvenform ein deutliches Indiz für eine Desorption nullter Ordnung.

Einzig im Bereich bis etwa 0,15 Monolagen ist der Sachverhalt ein anderer. Hier ist der Effekt der gemeinsamen Flankenbildung nicht erkennbar. Wie oben ausgeführt, liegen sogar die Desorptionsmaxima übereinander, was auf eine Desorptionsordnung von n=1 hinweist, wie schon Redhaed [RED62] zeigte. Er nutzt die konstante Maximumstem-peratur sogar aus, um mit ihrer Hilfe die Desorptionsenergie abzuschätzen. Im Bereich sehr kleiner Bedeckungen liegt also eine Desorption erster Ordnung vor.

 1.3.2 ‘Orderplots’

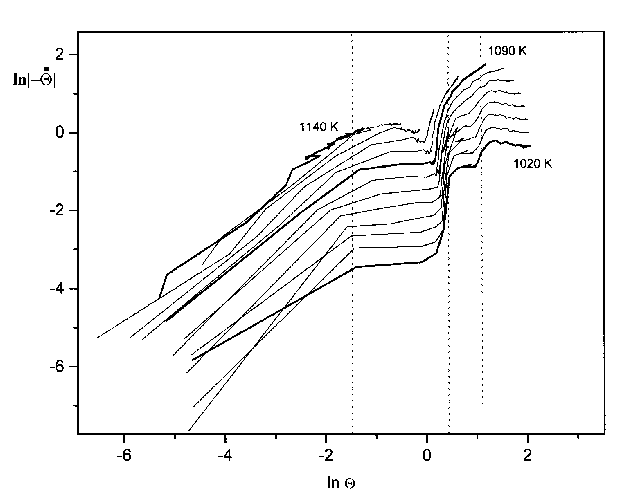
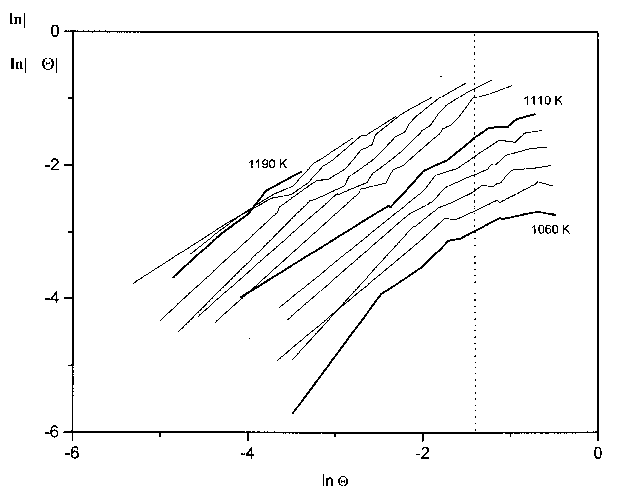
Abbildung 32 'Orderplots' aus den Thermodesorptionsspektren der Serie 3 für Bedeckungen zwischen 0,25 ML und 6ML

Abbildung 33 'Orderplots' aus den Thermodesorptionsspektren der Serie 9 für Bedeckungen zwischen 0,015ML und 0,29ML

Ein hilfreiches Mittel, um die Desorptionsordnung zu bestimmen, sind die bereits zuvor erwähnten sogenannte ‘Orderplots’. Nach Gleichung (34) liefert eine Auftragung des Logarithmus der Desorptionsrate über dem Logarithmus der Bedeckung für eine konstante Temperatur eine Gerade, aus deren Anstieg die Desorptionsordnung hervorgeht.

In Abb.32 sind jeweils vier Abschnitte zu erkennen, die einer gemeinsamen Steigung zuzuordnen sind. Besonders klar sind die Verhältnisse bei der Isotherme zu T=1020K. Diese hat drei Abschnitte, in denen der Anstieg null ist. Im letzten Teil (lnQ < -1,5) ist der Anstieg etwa eins. Die anderen Isothermen zeigen das gleiche Verhalten, mit der Einschränkung, daß mit steigender Temperatur die Anzahl der Gebiete mit konstanter Steigung abnimmt. Dies ist verständlich, wenn man bedenkt, daß mit ansteigender Temperatur mehr und mehr Zustände desorbieren und zur Darstellung nicht mehr beitragen können.

Der Submonolagenbereich ist in Abb.33 dargestellt. Besonders in der Isotherme zu T=1060K erkennt man einen (wenn auch langsamen) Steigungswechsel von eins auf null bei etwa lnQ=-1,5. Dieser Wert entspricht etwa einer Bedeckung von 0,22 Monolagen.

Zusammenfassend ist also festzustellen, daß für den Bereich Q<0,2ML eine Desorption erster Ordnung vorliegt. Mit dem Modell des 2D-Gases kann dies als der Bereich definiert werden, in dem die Adatome ausschließlich in der 2D-Gasphase vorliegen. Die Desorption ist deshalb erster Ordnung, weil sich während des Prozesses die Konzentration der desorbierenden Teilchen konstant ändert.

Ab Q=0,2ML wird die Desorptionsordnung null, bis eine Bedeckung von Q=1ML erreicht ist. Dieser Umstand deutet darauf hin, daß das System in die Region der Koexistenz 2D-Gas/Kondensat übergegangen ist. Die Desorption vollzieht sich hier aus einem Gleichgewicht und die Konzentration der desorbierenden Komponente ändert sich nicht. Den gleichen Verlauf der ‘Orderplots’ erhält Nagai [NAG86] für den Übergang von n=1 bzw. n=2 zu n=0.

Bereiche nullter Ordnung liegen ebenfalls für die zweite und dritte Monolage vor. Sie sind durch starke Steigungsänderungen in den ‘Orderplots’ voneinander getrennt. Das Modell des 2D-Gases kann hier nicht mehr gelten, da die Stellen der Oberfläche, die nicht durch Kupferatome der zweiten Lage besetzt sind, auch aus Kupferatomen bestehen, und zwar aus denen der ersten Lage. Gerade durch diese Atome aber wird die (Oberflächen-) Konzentration ebenfalls konstant gehalten. Voraussetzung dafür ist, daß alle Atome der zweiten Lage vor denen der ersten Lage desorbieren. Der relativ große Übergangsbereich von der ersten zur zweiten Lage könnte ein Indiz dafür sein, daß in diesem Bereich bereits vor der völligen Entleerung der zweiten Lage Atome der ersten Lage desorbieren.

Der Bereich der dritten bis n-ten (Lage) ist durch das Fehlen weiterer Steigungs-änderungen beim Übergang von einer Lage zur anderen und durch die Desorption nullter Ordnung gekennzeichnet. Daraus kann gefolgert werden, daß hier ein Wachs-tumsmodus vorliegt, bei dem nicht zwischen einzelnen Zuständen (Lagen) differenziert wird. Dies wäre bei der Ausbildung von 3D-Kristalliten der Fall.

Die vorliegenden Einzelfakten lassen sich zusammenfassen, indem ein Wachstums-modus ähnlich dem nach Stranski-Krastanov (vgl. I.2.2) konstatiert wird. Es bilden sich hier nacheinander zwei Lagen aus, auf denen dann Kristallite aufwachsen.

 1.4 Untersuchung der Desorptionsenergie und des Frequenzfaktors

1.4.1 Methode nach Redhead

Die Methode zur Abschätzung der Desorptionsenergie nach Redhead (vgl. I.3.1.5) ist sehr einfach und schnell durchführbar, um Aussagen über die Desorptionsenergie zu treffen. Als Voraussetzung wird gefordert, daß der Frequenzfaktor und die Desorptions-energie unabhängig von der Bedeckung sind. Hier wird der Fall einer Desorption erster Ordnung (mit einer konstanten Maximumstemperatur), also für Bedeckungen, die kleiner als 0,15ML sind, untersucht.

Die Größe des Frequenzfaktors wird vorgegeben (meistens n=10¹³s^-1»k_BT/h). Diese Näherung mindert natürlich die Güte dieses Verfahrens. Trotzdem kann es zu einer ersten Abschätzung dienen. Aus Abb.31 wurde als Maximumstemperatur für die ersten Thermodesorptionsspektren der Serie 9 ein Wert von T=1127K entnommen. Die daraus nach Gleichung (44) errechneten Desorptionsenergien (in Abhängigkeit von der Vorgabe des Frequenzfaktors n) sind in Tab.4 gegeben.

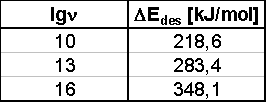
Tabelle 4 Desorptionsenergien nach Redhead

Wie ersichtlich sind die Werte stark von der Größe des Frequenzfaktors abhängig. Ein Wert von ca. DE_des=280kJ/mol soll hier als vorläufiges gemitteltes Ergebnis gelten.

 1.4.2 Heizratenvariation

Eine wesentlich höhere Qualität der Datenauswertung kann durch die Heizratenvariation erzielt werden (vgl. I.3.1.6). Hier ist es möglich, Desorptionsenergien und Frequenz-faktoren für Desorptionen beliebiger Desorptionsordnungen zu erhalten.

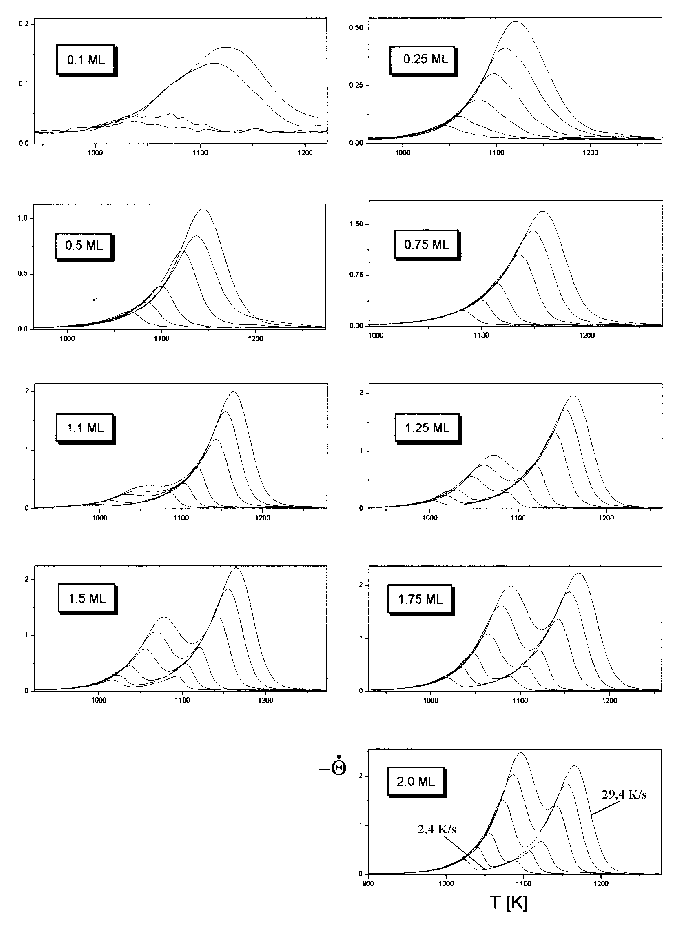
 Abbildung 34 Thermodesorptionsspektren der Serie 5 (s. Tab.3) J_ads=390°C; b=2,4; 4,3; 7,4; 14,7; 21,7; 29,4 K/s

Voraussetzung dafür ist, daß Serien von Thermodesorptionsspektren zu unterschied-lichen Heizraten aufgenommen werden. Das wurde in Serie 5 (Abb. 36) durchgeführt.

Aus diesen Spektren wurden die Temperaturen der Desorptionsmaxima für den b₂- und den b₃-Zustand zu den einzelnen Heizraten entnommen. Die so erhaltenen (zwei mal fünf) Wertepaare sind graphisch gegeneinander aufgetragen worden, und zwar in der Form lnT²/b=ƒ(1/T), entsprechend der Gleichung (45). Das Ergebnis ist in Abb.35 dargestellt.

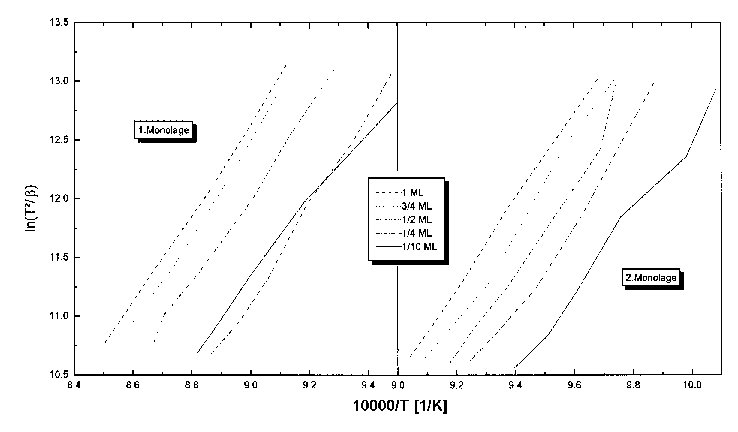
 Abbildung 35 Heizratenvariation von Serie 5

Durch eine lineare Regression der Datenpunkte konnten Geraden erhalten werden, aus deren Anstieg und Absolutglied nach (45) sowohl die Desorptionsenergie als auch der Frequenzfaktor in Abhängigkeit von der Bedeckung errechnet wurden.

 Beim Vergleich dieser Spektren für die Desorptionsenergie und den Frequenzfaktor (s. Abb.36) fällt zunächst der äquivalente Kurvenverlauf auf, der auf einen starken Kompensationseffekt zwischen diesen beiden Größen hinweist (vgl. I.2.1.2, Gleichung (7)).

Die Kurven für den Bereich der ersten Lage lassen sich in zwei Gebiete einteilen. Bis 0,2ML ist ein starker Anstieg von DE_des von 260kJ/mol auf 320kJ/mol und von n von 10¹²s^-1 auf 10¹⁴s^-1 zu verzeichnen. Der Anstieg des Frequenzfaktors ist damit zu erklären, daß die im Modell geforderten idealen Gaseigenschaften mehr und mehr durch intermolekulare Wechselwirkungen beeinträchtigt werden. (Für die Interpretation der Energiewerte vgl. 1.4.6.)

Im zweiten Bereich der ersten Lage bleiben der DE_des-Wert mit 320kJ/mol und der Frequenzfaktor mit 3x10¹⁴s^-1 konstant.

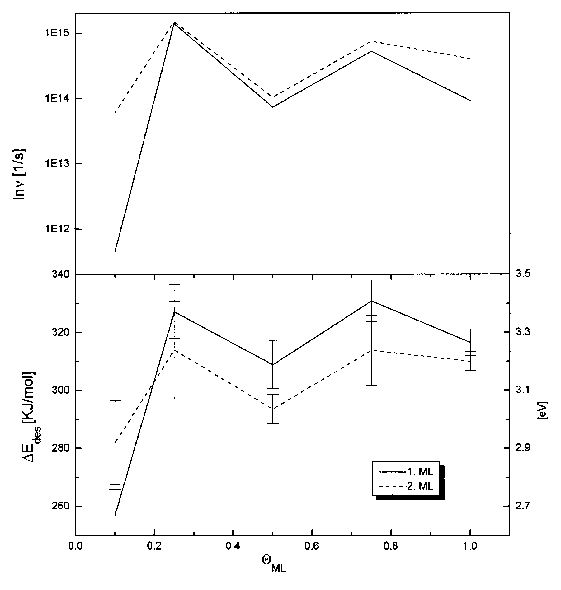
 Abbildung 36 Heizratenvariation von Serie 5

Im gesamten Bereich der zweiten Lage ist dann ein schwacher Anstieg der Desorptionsenergie von 290kJ/mol auf 310kJ/mol zu verzeichnen. Der Wert des Frequenzfaktors liegt im gesamten Bereich konstant bei 3x10¹⁴s^-1.

 1.4.3 Methode nach Bauer

Eine sehr präzise Auswertungsmethode stellt das Verfahren nach Bauer dar (vgl. I.3.1.8). Die Desorptionsenergie und der Frequenzfaktor können bei dieser Methode bedeckungsgradabhängig sein. Die Desorptionsordnung kann bei diesem Verfahren beliebig sein.

Um zu verläßlichen Ergebnissen zu gelangen, ist es erforderlich, Spektren in möglichst kleinen Bedeckungsgradschritten aufzuzeichnen. Hier soll der Bereich bis zu zwei Lagen untersucht werden. Zu diesem Zweck wurden die Thermodesorptionsspektren der Serie 6 aufgenommen (s. Abb.37).

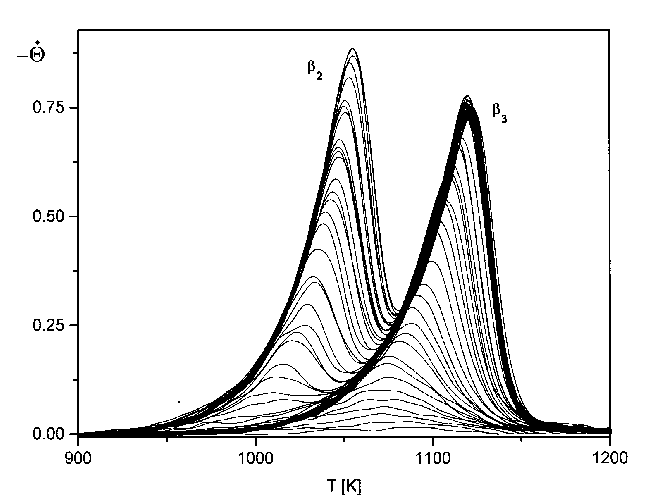
 Abbildung 37 Thermodesorptionsspektren der Serie 6 (s. Tab.3) J_ads=390°C; b=7,7K/s

Das Bauersche Verfahren, das ursprünglich der graphischen Auswertung diente, wurde hier rechnergestützt durchgeführt.

Um die zur Desorptionsrate gehörige Bedeckung zu erhalten, wurden als zweiter Schritt alle Spektren von der Hochtemperaturseite her integriert (s. Abb.38). Aus den Wertepaaren (- Q) konnte die Lebensdauer t nach Gleichung (49) berechnet werden. Das Ergebnis ist in Abb.39 als Funktion lnt=ƒ(Q) dargestellt.

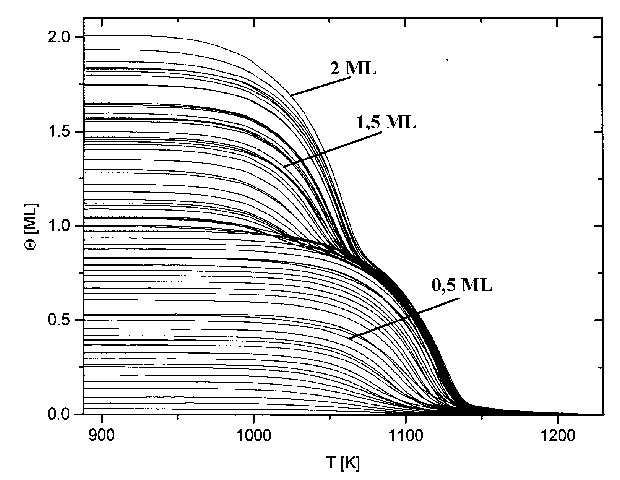
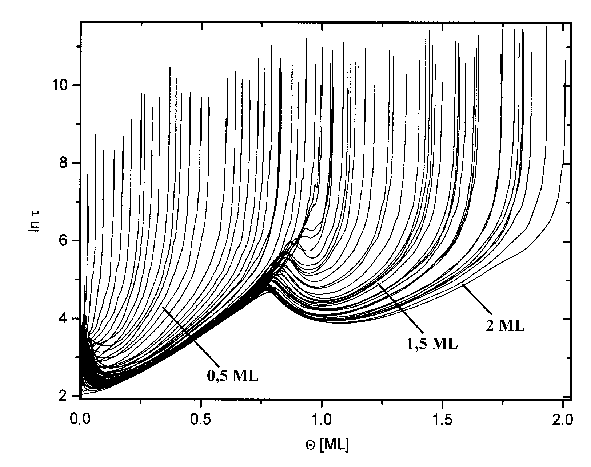
 Abbildung 38 Temperaturabhängigkeit des Bedechungsgrades für Spektren der Serie 6

Abbildung 39 Bedeckungsgradabhängigkeit der Lebensdauer für Spektren der Serie 1 (s. Tab.3) J_ads=570°C; b=4,1K/s

Um den Rechenaufwand in sinnvollen Grenzen zu halten, wurde weiterhin für jedes Spektrum der Bedeckungsgradbereich (zwei Monolagen) mit einer Schrittweite von 0,01ML unterteilt.

Einem jedem solchen Bedeckungswert wird nun sein lnt-Wert zugeordnet, ebenso sein Temperaturwert. Als nächster Schritt werden die Wertetripel (Q; lnt; T) nach der Temperatur umsortiert. Für die Werte der ersten Lage wurden die der zweiten Lage dabei nicht mit berücksichtigt. Aus einer Darstellung von lnt in Abhängigkeit von der Temperatur erhält man die ‘Arrheniusgeraden’ und zwar eine für jedes Spektrum. Da der Anstieg dieser Geraden die Desorptionsenergie beinhaltet und in deren Absolutglied der Frequenzfaktor enthalten ist, erhält man das Wertetripel (Q₀; DE_des; n) für jedes Spektrum.

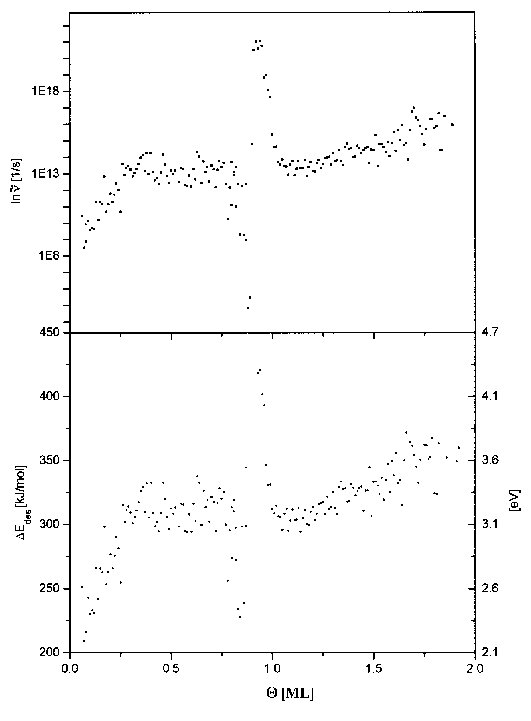
 Abbildung 40 Desorptionsenergie und Frequenzfaktor für die ersten beiden Lagen (aus Spektren der Serie 6)

Die Ergebnisse der Auswertung sind in Abb.40 als Darstellung des Verlaufs der Desorptionsenergie und des Frequenzfaktors über der Anfangsbedeckung gegeben.

Auch hier sind für Bedeckungen oberhalb von 0,25ML die Desorptionsenergie und der Frequenzfaktor konstant (DE_des=305kJ/mol, n=10¹³s^-1). Im Bereich davor ist ein Anstieg der Werte zu verzeichnen und zwar für DE_des ab 220kJ/mol und für n ab 10⁹s^-1. Im Bedeckungsbereich von 1 bis 2ML steigt die Desorptionsenergie von 300kJ/mol auf 360kJ/mol und der Frequenzfaktor von 10¹³s^-1 auf 10¹⁶s^-1 an.

Im Bereich von 0,8 bis 1,0ML treten, abweichend von den Ergebnissen der Heizratenvariation, zusätzliche Effekte auf. Hier sinkt die Desorptionsenergie zunächst auf einen Wert von 220kJ/mol, um dann rasch auf einen Wert von 410kJ/mol anzusteigen. (Der Frequenzfaktor sinkt auf 10⁶s^-1 und steigt danach auf 10²²s^-1 an.) Bei der Vollendung der ersten Lage haben sich beide Werte dem Ausgangszustand wieder angeglichen.

Zur genaueren Untersuchung des Submonolagenbereichs wurden aus den Spektren der Serie 9 ebenfalls die Energiewerte und Frequenzfaktoren errechnet. Dieser Bereich ist in Abb. 41 dargestellt.

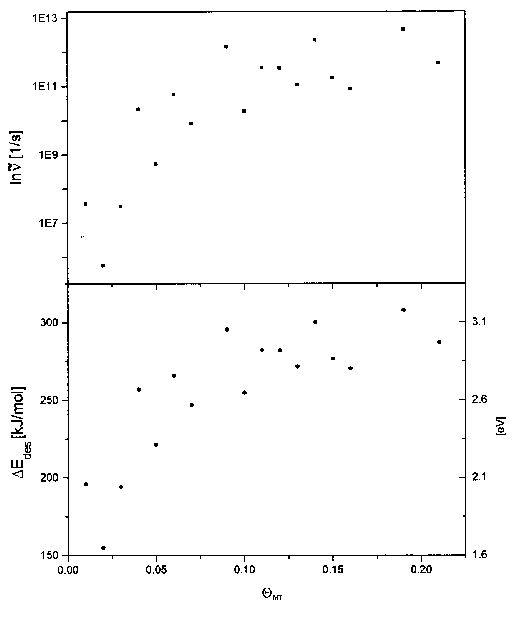
Abbildung 41 Desorptionsenergie und Frequenzfaktor

für den Bereich des 2D-Gases (aus Spektren der Serie 9)

Der aus Abb. 40 schon bekannte Verlauf bestätigt sich hier im wesentlichen. Es ist ein exponentieller Anstieg der Kurven erkennbar. Die größten Änderungen vollziehen sich im Bereich bis 0,15ML. Die Desorptionsenergie steigt bis dahin von 180kJ/mol auf 280kJ/mol an. Gleichzeitig steigt auch der Frequenzfaktor von 10⁷s^-1 auf 10¹¹s^-1.

Zustandsseparation

Kontroverse Meinungen bestehen darüber, ob die Zustände der Thermodesorptions-spektren vor der Berechnung der Desorptionsenergie separiert werden sollen oder nicht ([BAU74] pro, [BAU75] contra). Es besteht nämlich die Möglichkeit, daß es bei Q_ML»1 zu Interschichtwechselwirkungen kommt, d.h., daß bereits Teilchen aus einer unteren Lage desorbieren, obwohl sich auch noch Teilchen in der höheren Lage befinden. Dieser Effekt tritt z.B. bei Systemen wie Ag/Re(0001) auf [SCH97], wo das Adsorbat eine größere Gitterkonstante besitzt als das Substrat und es zu starken Spannungen im Adsorbatgitter bei der Ausbildung einer (besonders der ersten) Lage kommt.

Um zu entscheiden, welche Vorgehensweise in diesem Fall zu bevorzugen ist, wurde die Separation für die Serie 6 (vgl. I.3.1.2) ausgeführt.

Als einfache Näherung kann dazu die Gleichung (32) verwendet werden. Die Separation des b₂- vom b₃-Zustand ist sinnvoll und erlaubt, da beide recht gut aufgespalten sind. Für den b₃-Zustand braucht kein Rechenaufwand betrieben zu werden; hier können die Spektren des b₂-Zustandes einfach unberücksichtigt bleiben.

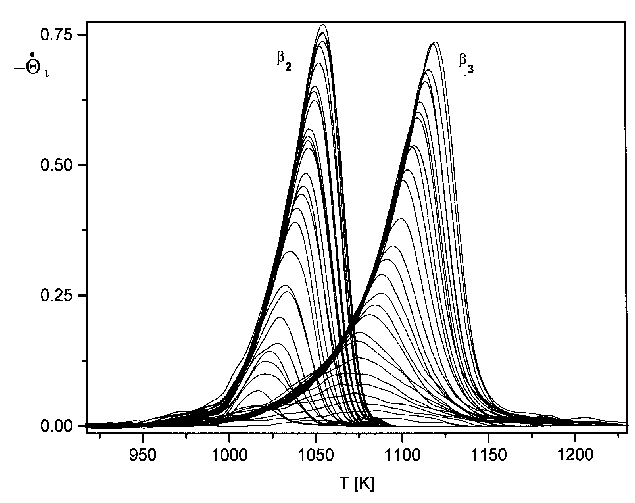
 Abbildung 42 Seperation des b₂- und b₃-Zustandes für Spektren der Serie 6

Zunächst sind einige kurze Bemerkungen zum Verlauf der Kurven nötig. Besonders für den b₂-Zustand ergibt sich aus der Separation gegenüber der Ursprungsserie (Abb.38) eine wichtige Konsequenz. Es zeigt sich, daß die Spektren des b₂-Zustandes eine fast symmetrische Form haben. He et al [HEG90] räumen die Möglichkeit ein, daß es sich um eine Desorption erster Ordnung mit starken attraktiven Wechselwirkungen handeln könnte. Der Umstand, daß alle Spektren in einer gemeinsamen Anstiegsflanke bis zu T_g ansteigen, ist aber auch hier gegeben, und es soll auch weiterhin von einer Desorption nullter Ordnung für den b₂-Zustand ausgegangen werden.

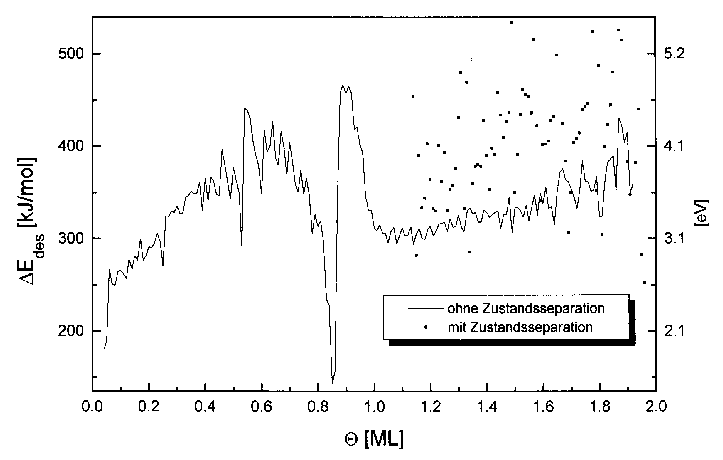
Abbildung 43 Bauersche Desorptionsenergieauswertung

Aus den Spektren für den b₂-Zustand wurden die Desorptionsenergiewerte nach dem o.a. Verfahren ermittelt. Es zeigte es sich, daß die Daten erheblich streuten und deren Mittelwert deutlich über dem aus der Rechnung der nicht separierten Spektren lag.

Dieser Befund führt zu der Behauptung, daß eine Zustandsseparation für das System Cu/Re(0001) nicht günstig ist.

 1.4.4 Methode nach King

Die Auswertungsmethode nach King (vgl. I.3.1.7) unterscheidet sich letztlich nur unwesentlich von der nach Bauer. Hier wird nicht mit lnt, sondern statt dessen mit gearbeitet, was die graphischen Auswertungen durchaus unterscheidet. Bei der rechnergestützten Auswertung ergeben sich aber kaum Unterschiede. Die erhaltenen Werte weichen tatsächlich kaum von denen der Bauerschen Methode ab, teilweise sind sie sogar identisch (s. Abb.45).

 1.4.5 Methode nach Habenschaden und Küppers

Eine grundsätzlich andere Methode ist von Habenschaden und Küppers [HAB83] (vgl. I.3.1.9) entwickelt worden. Sie stützt sich auf die Auswertungsmethode für Desorp-tionen nullter Ordnung nach Polanyi (vgl. I.3.1.4). Für jedes Spektrum wird der natürliche Logarithmus der Desorptionsrate in Abhängigkeit von der reziproken Temperatur aufgetragen. Es ergibt sich eine Gerade, aus deren Anstieg direkt die Desorptionsenergie errechnet wurde. Im Unterschied zum Polanyischen Verfahren wird hier nicht der gesamte Spektrenverlauf betrachtet, sondern nur der Bereich bis der Niedertemperaturflanke.

Es sind zunächst die Spektren der Serie 6 der Auswertung unterzogen worden (s. Abb.45). Der eigentliche Vorteil dieser Methode ist allerdings der, daß auf Grund des kleinen betrachteten Q-Bereiches, jegliche Wechselwirkung der einzelnen Desorptions-zustände ausgeschlossen werden kann. Es ist somit möglich, mit relativ hoher Genauigkeit Desorptionsenergiewerte auch für hohe Bedeckungen zu erhalten. Nachteilig ist allerdings das schlechtere Signal-zu-Rausch-Verhältnis der betrachteten kleinen Flankenabschnitte.

Diese Methode wurde weiterhin auf die Spektren der Serien 4 und 8 angewendet, s. Abb.44.

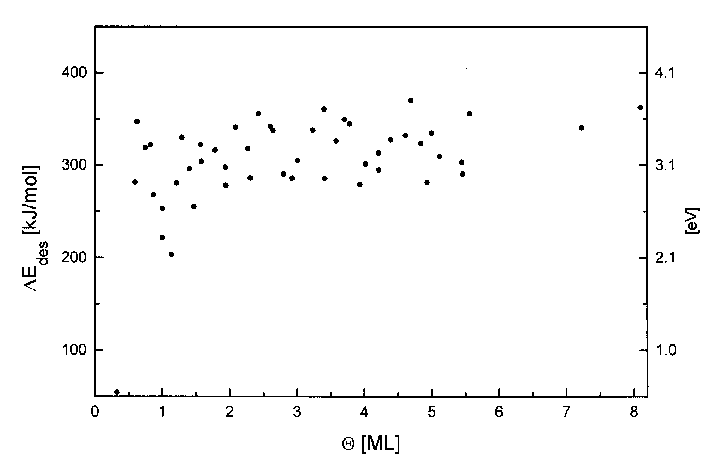
 Abbildung 44 Desorptionsenergie für Spektren der Serie 4 und 8 (Tab. 3) nach Habenschaden/Küppers

Die Desorptionsenergie liegt im Bereich ab 2ML konstant bei 305kJ/mol. Dieser Wert korreliert mit den Literaturwerten für die Sublimationsenthalpie (s. Tab.1). Im Bereich davor treten starke Änderungen der Desorptionsenergie auf, auf die im nächsten Abschnitt eingegangen werden soll.

 1.4.6 Gemeinsame Betrachtung der Auswertungsmethoden

Zum besseren Vergleich sind in Abb. 45 die Desorptionsenergiewerte nach den verschiedenen Auswertungsmethoden in Abhängigkeit vom Bedeckungsgrad dar-gestellt.

Zunächst soll der Verlauf der Desorptionsenergie im Bereich bis zwei Lagen diskutiert werden, der aus der gemeinsamen Betrachtung der Werte aller Verfahren erhalten wurde. Danach wird auf Besonderheiten im Verlauf der Desorptionsenergie eingegan-gen und abschließend soll die Abweichung der Werte der verschiedenen Verfahren diskutiert werden.

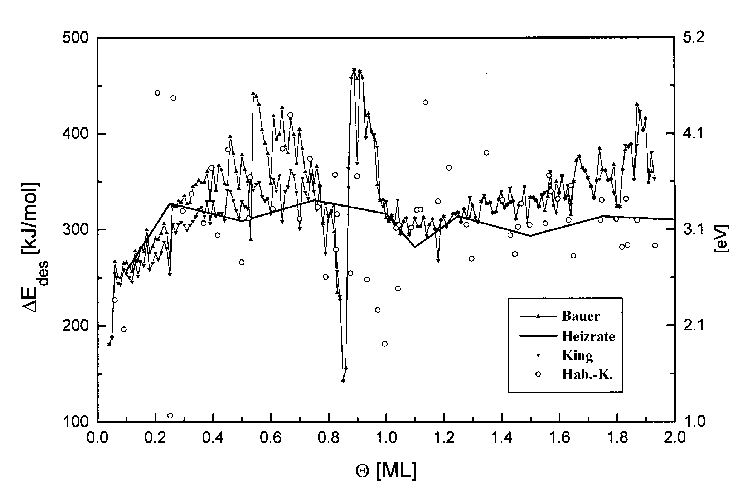
 Abbildung 45 Desorptionsenergien für Spektren der Serie 6, nach Bauer [BAU75], King [KIN75], Habenschaden/Küppers [HAB83] und aus der Heizratenvariation

a) Beurteilung der Ergebnisse

Im Bereich bis ¼ ML steigen die zunächst sehr niedrigen Energiewerte mit dem Bedeckungsgrad stark, nämlich von 180kJ/mol auf etwa 310kJ/mol an. (Dieser Verlauf ergab sich auch aus der Untersuchung des Submonolagenbereichs (Serie 9) mit dem Bauerschen Verfahren (s. Abb. 41).)

Niedrige Desorptionsenergien kennzeichnen die Desorption aus der 2D-Gasphase. Die Teilchen besitzen bereits eine gewisse Energie, um sich frei auf der Oberfläche bewegen zu können. Diese Beweglichkeit wird jedoch mit zunehmender Bedeckung einge-schränkt, da sich attraktive Wechselwirkungen ausbilden und zunehmen. Nach Gleichung (53) muß ebenfalls die Wechselwirkungsenergie E_WW überwunden werden, damit Teilchen desorbieren können. Die Bindungsenergie wird damit größer. Es muß mehr Energie aufgewendet werden, damit die Teilchen desorbieren können.

Der Bereich von ¼ ML bis 1ML ist durch einen konstanten Wert 330kJ/mol für die Desorptionsenergie gekennzeichnet. (Der Bereich bei etwa 1ML wird später behandelt.) Dieser Bereich ist durch die Desorption aus einem Gebiet gekennzeichnet, in dem sowohl 2D-Gasteilchen als auch kondensierte Teilchen vorliegen. Diese Teilchen üben auf Grund der größeren Dichte der Komponente stärkere Wechselwirkungen aufeinander aus.

Der Literaturwert von 389kJ/mol für die Desorptionsenergie von Cu auf Re(0001) [ROD91], [HEG90] weicht erheblich von der o.a. Energie ab. Das rührt daher, daß dort nach dem Verfahren von Polanyi , was natürlich Schwächen aufweist, gearbeitet wurde. Außerdem sind diese Spektren mit einer sehr hohen Heizrate aufgenommen worden, was die ‘Deutlichkeit’ der Kurven beeinträchtigt. Es wurde weiterhin auch kein Kurvenverlauf angegeben, sondern nur ein (wahrscheinlich gemittelter) Wert.

Als weitere Literaturwerte für die Desorptionsenergie von Cu auf Metalloberflächen sind 405kJ/mol [BAU74] und 347kJ/mol [GOL86] für das System Cu/W(110) sowie 338kJ/mol [BAU87] für das System Cu/Mo(110) anzuführen. Die Wechselwirkungen von Kupfer mit den betrachteten Substraten W, Mo ist größer als die mit Re. Beide Substrate sind elektronenärmer als Cu und Re und somit kann ein stärkerer Charge-Transfer-Effekt zwischen Kupfer und den Substraten erwartet werden.

Für das System Ag/Re(0001) wird ein Wert von 293kJ/mol angegeben [SCH97] und für Pd/Re(0001) ein Wert von 414kJ/mol. Silber hat zwar eine ähnliche Elektronenkon-figuration wie Kupfer, jedoch ist sein Atomradius von r=1,44Å [SHR91] größer als der von Rhenium r=1,38Å. Natürlich stimmt auch der Radius des Kupferatoms r=1,28Å [WEA74] nicht mit dem des Rheniums überein, doch ist beim Silber auf Grund der positiven Fehlanpassung eher von einer repulsiven Wechselwirkung auszugehen. Diese Wechselwirkungen führen zu einer Lockerung der Bindung zum Substrat, woraus die niedrigere Desorptionsenergie resultiert.

Der Bereich der zweiten Lage ist durch eine konstante Desorptionsenergie in Höhe von 310kJ/mol gekennzeichnet. Die Wechselwirkungen mit dem Substrat haben bereits merklich an Einfluß verloren, und es werden hauptsächlich Desorptionsenergien in Höhe der Sublimationsentropie des Kupfers erhalten (s. Tab.1).

Der Literaturwert von He et al [HEG90] und [ROD91] ist 310kJ/mol für Cu/Re(0001). Dieser Wert stimmt genau mit unserem Meßwert überein. Weitere Literaturwerte sind in Tabelle 6 angegeben.

b) Der Bereich 0,8ML£Q£1,1ML

Der Abfall der Desorptionsenergie auf Werte um 200kJ/mol bei 0,85ML (Bauer+King) bzw. bei 1ML (Hab.-K.) und der darauf folgende Anstieg auf Werte um 450kJ/mol im Bereich von etwa 0,8ML bis 1,1ML, die auch für das Systems Cu/W(110) beobachtet wurden [BAU74], können auf unterschiedliche Art und Weise diskutiert werden:

1. Man kann sich auf den Standpunkt stellen, daß die Desorptionsenergieänderungen Artefakte sind, die sich aus der Konstruktion der Arrheniusplots ergeben. Hierbei werden nämlich einige Effekte, wie z.B. das Auftreten von mehr als einem Adsorptionsplatz, laterale Wechselwirkungen, Desorption nicht aus Ungleichge-wichtszuständen und Temperaturabhängigkeiten [KRE91], [PAY93] nicht berück-sichtigt. Dafür spricht auch das Auftreten der Schwankungen bei unterschiedlichen Bedeckungen in Abhängigkeit von der angewendeten Auswertungsmethode. Außerdem sind die Energieänderungen bei der Heizratenvariation überhaupt nicht zu erkennen.
2. Die Effekte werden als physikalisch real betrachtet und als Konsequenz des Kompensationseffektes zwischen der Desorptionsenergie und dem Frequenzfaktor, der die Desorptionsentropie beinhaltet, beschrieben. Dazu muß man beachten, daß die Desorptionsenergie sowohl den entropischen als auch den enthalpischen Beitrag zur Desorption beinhaltet. Der Abfall der Kurven wäre dadurch erklärbar, daß mit Vollendung der ersten Lage die Adatome immer dichter zusammenrücken und das Mißverhältnis der Gitterkonstanten sehr stark in Form von Spannungen zum Ausdruck kommt. Der Effekt des darauffolgenden Anstieges könnte eventuell aus enthalpischer Sicht beschrieben werden. Ginge man von der Voraussetzung aus, daß die erste Lage vollständig gefüllt ist, bedeutete dies, daß jedes Adatom vollständig lokalisiert ist. Daraus folgte ein enormer Anstieg der Desorptionsentropie vom Zustand der totalen Ordnung zu einem Zustand totaler Unordnung (Differenz der Entropie des (idealen) 3D-Gases und der Entropie des Systems Adsorbat/Substrat). Dafür spricht die für dabei auftretende Frequenzfaktoren (n=10²²s^-1) berechnete Desorptionsentropie in der Größenordnung der Sublimationsentropie des reinen Kupfers (s. Tab.5).
3. Aber auch Wechselwirkungen der einzelnen Lagen untereinander sind möglich [BAU87]. Bevor die erste Lage vollständig aufgefüllt ist, könnten Atome in die zweite Lage eingebaut werden. Bei der Desorption können ebenfalls Atome der ersten Lage desorbieren, bevor die zweite Lage vollständig desorbiert ist. Dies ist z.B. beim System Ag/Re(0001) der Fall, wo allerdings das Adsorbat die größere Gitterkonstante hat [SCH97].

Eine endgültige Klärung dieser Effekte kann hier nicht gegeben werden. Wir verweisen in diesem Zusammenhang auf (nicht nur eigene) zukünftige Arbeiten und diskutieren diese Desorptionsenergieänderungen vorerst nicht weiter.

c) Vergleich der Auswertungsmethoden

Abschließend soll die Genauigkeit der einzelnen Methoden, die sich nach dem jeweils untersuchten Bedeckungsbereich unterteilen lassen, beurteilt werden. Bei den Methoden nach King und Bauer wird nicht nur der gesamte Spektrenbereich der Analyse unterzogen, sondern auch mehrere Spektren einer Serie. Daraus resultiert ein geringes Rauschen der Daten, aber Effekte z.B. beim Übergang zwischen zwei Lagen (s.o.) fallen besonders stark ins Gewicht. Die Methode nach Habenschaden und Küppers untersucht nur den ersten kleinen Teil der Niedertemperaturflanke eines Spektrums, ist damit frei von Wechselwirkungen, jedoch sehr rauschempfindlich. Bei der Heizratenvariation wird jeweils die Maximumstemperatur zur Rechnung benutzt. Andere Spektren können, allerdings nicht sehr stark wechselwirken. Auf Grund der hohen Signalintensität besitzt diese Methode ein besonders gutes Signal-zu-Rausch-Verhältnis.

Das Abweichen der Energien zwischen dem Bauerschen und dem Kingschen Verfahren bei mittleren Bedeckungsgraden der ersten Lage sind als Artefakt einzustufen. Sie resultieren wohl aus einer notwendigen Glättung der Daten innerhalb der Methode nach Bauer.